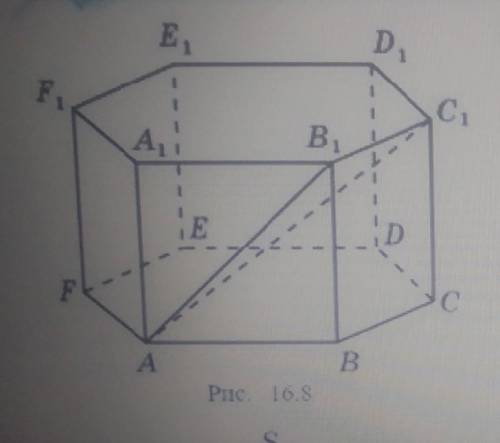
В правильной шестиугольной призме ABCDEFA B1C1D1E1F1 все ребра равны 1. Найдите угол между: а)прямой АВ1 И ПЛОСКОСТЬЮ АВС; б)прямой АС1 И ПЛОСКОСТЬЮ АВС; прямой АА1 и плоскостью АСD1.​

Для того чтобы решить эту задачу, нам понадобятся некоторые знания о геометрии и свойствах правильных многогранников.

Перед тем, как перейти к решению, давайте разберем, что такое правильная шестиугольная призма. Это многогранник, у которого основание является правильным шестиугольником, и все его грани являются прямоугольными.

Теперь мы можем перейти к решению задачи.

а) Найдем угол между прямой АВ1 и плоскостью АВС.

Для этого нам нужно знать, что прямая, перпендикулярная к плоскости, проходит через центр основания призмы. Основание призмы ABCDEF является правильным шестиугольником, поэтому центр основания совпадает с его центром.

Чтобы найти угол между прямой АВ1 и плоскостью АВС, нам нужно найти угол между прямой АВ1 и перпендикулярной к ней линией, проведенной через центр основания призмы.

Обратите внимание, что в правильном шестиугольнике центр делит прямую, соединяющую противоположные вершины, пополам. Это означает, что AB1 = AB.

Теперь мы можем рассмотреть прямоугольный треугольник АBC. В этом треугольнике прямой угол при вершине B равен 90 градусам, а стороны AB и BC равны 1.

Мы можем использовать теорему Пифагора, чтобы найти сторону AC треугольника АBC:
AC^2 = AB^2 + BC^2
AC^2 = 1^2 + 1^2
AC^2 = 2
AC = √2

Теперь мы можем рассмотреть прямоугольный треугольник AB1C1. В этом треугольнике у нас есть гипотенуза AC = √2 и одна из катетов AB1 = AB = 1. Мы можем использовать основное тригонометрическое соотношение sin α = противолежащая / гипотенуза, чтобы найти угол α между прямой АВ1 и плоскостью АВС:

sin α = AB1 / AC
sin α = 1 / √2
α = arcsin(1 / √2)

Таким образом, угол α между прямой АВ1 и плоскостью АВС равен arcsin(1 / √2).

б) Найдем угол между прямой АС1 и плоскостью АВС.

Аналогично предыдущему пункту, прямую, перпендикулярную к плоскости, можно провести через центр основания призмы. Так как центр основания совпадает с центром шестиугольника ABCDEF, мы можем провести прямую через центр и вершину С1.

Для того чтобы найти угол между прямой АС1 и плоскостью АВС, мы можем рассмотреть прямоугольный треугольник АС1С. В этом треугольнике прямой угол при вершине С равен 90 градусам, а стороны AC1 и СC1 равны 1.

Мы можем использовать теорему Пифагора, чтобы найти сторону АС треугольника АС1С:
AC^2 = AC1^2 + CC1^2
AC^2 = 1^2 + 1^2
AC^2 = 2
AC = √2

Теперь мы можем рассмотреть прямоугольный треугольник AC1C. В этом треугольнике у нас есть гипотенуза АС = √2 и одна из катетов AC1 = 1. Мы можем использовать основное тригонометрическое соотношение sin β = противолежащая / гипотенуза, чтобы найти угол β между прямой АС1 и плоскостью АВС:

sin β = AC1 / AC
sin β = 1 / √2
β = arcsin(1 / √2)

Таким образом, угол β между прямой АС1 и плоскостью АВС равен arcsin(1 / √2).

в) Найдем угол между прямой АА1 и плоскостью АСD1.

Прямую, перпендикулярную к плоскости АСD1, тоже можно провести через центр основания призмы. Центр основания совпадает с центром шестиугольника ABCDEF, поэтому прямая пересечения АА1 и плоскости АСD1 также проходит через центр основания.

Она будет перпендикулярна прямой АС1, поскольку прямая АА1 является диагональю прямоугольника АC1D1F1.

Таким образом, угол между прямой АА1 и плоскостью АСD1 равен 90 градусов.

Надеюсь, эти подробные объяснения помогли вам понять, как найти углы между данными прямыми и плоскостями в данной задаче. Если у вас остались какие-либо вопросы, не стесняйтесь задавать их.