В основании пирамиды лежит прямоугольный треугольник с катетами 15 и 15√3. Каждое боковое ребро пирамиды наклонено к плоскости основания под углом arctg2√3 / 225. Найдите объем пирамиды

Пошаговое объяснение:

ДАНО:  ПИРАМИДА

ΔАВС- прямоугольный

АВ=15,   ВС=15√3

∠a =arctg(2√3)/225

НАЙТИ:   Vпирамиды

V= 1/3 Sосн*h

1) ΔABC  прямоугольный  AB, BC катеты,  Sосн=1/2*AB*BC  

2) Высота пирамиды "h", опущенная из вершины D, в точку "0",  причем  "0" является точкой центром описанной окружности  ΔАВС,  то есть, точкой пересечения срединных перпендикуляров, проведенных к сторонам ΔАВС.(в часном случае ΔАВС прямоугольный, и "О" лежит на гипотенузе АС )

Δ  ΔОЕВ - прямоугольный , с катетами "ОЕ"  "ОМ"  и дпины их  равны половине соответствующих катетов ΔАВС   OB²=OE²+OM²=1/4(AB²+BC²)

Из ΔDBO  Прямоугольный, известен катет и прилежащий угол,

∠a нам дан.  tg∠a= OE/OB       OE=OB/tg∠a

рабочая формула будет иметь вид

V=1/3 *1/2*AB*BC* h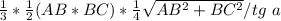    

как то так

калькулятор в