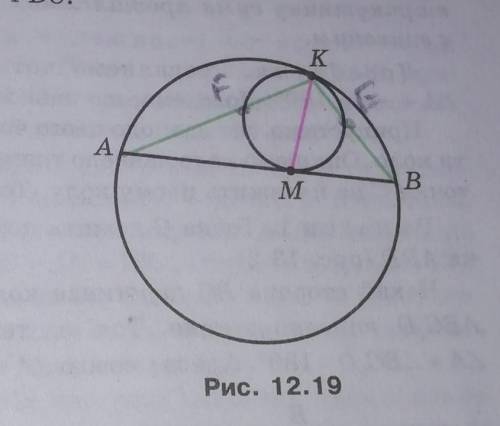
В окружности проведено хорду AB. Другая окружность касаеться этой хорды в точке М и к заданой окружности в точке К. Докажите что KM биссектриса угла

Добро пожаловать в наш урок, где мы будем доказывать, что линия KM является биссектрисой угла.

Давайте разберемся сначала, что такое биссектриса угла. Биссектриса угла - это линия, которая делит данный угол на два равных угла. В данном случае, мы должны доказать, что линия KM делит угол BKM на два равных угла.

Для начала, давайте обратим внимание на свойство касательной окружности. Известно, что из точки касания, линия, соединяющая это точку с центром окружности, будет перпендикулярна касательной. То есть, линия KM будет перпендикулярна касательной, проведенной из точки K.

Теперь, чтобы доказать, что KM - биссектриса угла BKM, нам нужно показать, что угол MBK равен углу MCK. Для этого, рассмотрим треугольник MKB и треугольник MKC.

В треугольнике MKB, у нас есть сторона MK, которая равна стороне MK (по определению частичного касания - когда меньшая окружность касается большей окружности внутренним образом), сторона KB, которая равна стороне KC (как радиусы касающихся окружностей) и сторона МB, которая равна стороне МC (как радиусы касающихся окружностей).

Теперь давайте взглянем на углы. У нас есть угол BKM и угол KMB, которые являются вертикальными углами и, следовательно, равны друг другу. Угол BMK является прямым углом, так как KM перпендикулярна касательной в точке K. А угол BKM мы хотим доказать, что он равен углу MCK.

Таким образом, по стороне - углу - стороне (SAS) по теореме о равенстве треугольников, треугольник MKB и треугольник MKC равны друг другу. Следовательно, угол MBK равен углу MCK.

Исходя из этого, мы можем заключить, что линия KM делит угол BKM на два равных угла и, следовательно, является биссектрисой угла.