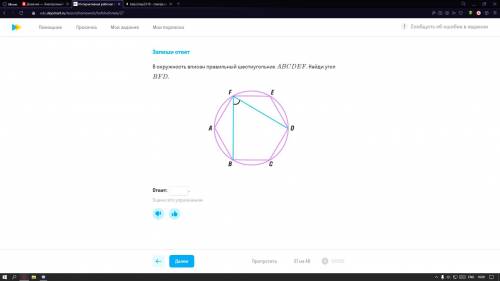
В окружность вписан правильный шестиугольник abcdef. найдите угол bfd

Пошаговое объяснение:

Мне кажется , что возможно тут ответ будет 60°

Для решения данной задачи, нам понадобятся знания о свойствах окружностей и правильных многоугольников.

1. Заметим, что правильный шестиугольник имеет все стороны и углы равными. Поэтому каждый угол шестиугольника abcdef будет равен 360° / 6 = 60°.

2. Также, из свойств правильных многоугольников, следует, что вписанный угол в окружность равен половине центрального угла, опирающегося на ту же дугу. Следовательно, для нахождения угла bfd нам нужно найти центральный угол, опирающийся на дугу bf.

3. Заметим, что нужный часть окружности находится между точками b и d. Так как построен правильный шестиугольник, то его центр совпадает с центром окружности. Поэтому, чтобы найти половину центрального угла, мы должны найти половину дуги bf.

4. Чтобы найти половину дуги bf, мы должны найти угол, опирающийся на эту дугу. В данном случае это угол bcd. Заметим, что угол bcd является внешним по отношению к треугольнику bfd. Согласно свойству внешних углов треугольника, он равен сумме двух внутренних углов. В данном случае это углы fbd и bfd.

5. Углы fbd и bfd равны, так как они являются углами правильного шестиугольника. Из пункта 1 мы знаем, что угол правильного шестиугольника равен 60°. Следовательно, углы fbd и bfd будут равны 60° / 2 = 30° каждый.

6. Теперь у нас есть угол bcd, которому соответствует половина дуги bf, и два угла fbd и bfd, равных 30° каждый. Чтобы найти половину дуги bf, мы должны сложить углы fbd и bfd. Получаем 30° + 30° = 60°.

7. Таким образом, половина дуги bf равна 60°. Следовательно, угол bfd будет равен удвоенной величине половины дуги bf: 2 * 60° = 120°.

Ответ: Угол bfd равен 120°.