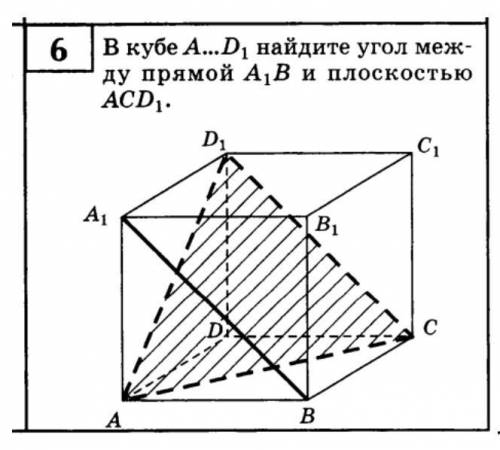
В кубе A...D1 найдите угол между прямой A1B и плоскостью ACD1

Чтобы найти угол между прямой A1B и плоскостью ACD1, нам понадобится использовать понятие скалярного произведения векторов. 1. Найдем векторы, лежащие на прямой A1B и плоскости ACD1: Вектор, лежащий на прямой A1B, можно найти, вычитая координаты начальной точки (A1) из координат конечной точки (B). Обозначим этот вектор как v1: v1 = B - A1 Векторы, лежащие в плоскости ACD1, можно найти, вычитая координаты начальной точки (A) из координат других точек в плоскости. Обозначим два таких вектора как v2 и v3: v2 = C - A v3 = D1 - A 2. Выполним скалярное произведение вектора v1 на векторы v2 и v3: Скалярное произведение векторов определяется следующей формулой: a · b = |a| * |b| * cos(θ) где a и b - скаляры, |a| и |b| - длины векторов, θ - угол между векторами. Для нахождения угла между прямой A1B и плоскостью ACD1, мы сначала найдем скалярное произведение вектора v1 на вектор v2, а затем на вектор v3. Обозначим эти скалярные произведения как s1 и s2: s1 = v1 · v2 s2 = v1 · v3 3. Найдем длины векторов v1, v2 и v3: Длина вектора определяется формулой: |a| = √(a1^2 + a2^2 + a3^2) где a1, a2, a3 - координаты вектора. Обозначим эти длины как |v1|, |v2| и |v3|. 4. Найдем угол между прямой A1B и плоскостью ACD1: Используя скалярные произведения s1 и s2, а также длины векторов |v1|, |v2| и |v3|, мы можем найти угол между прямой A1B и плоскостью ACD1 с помощью следующей формулы: cos(θ) = (s1 + s2) / (|v1| * √(|v2|^2 + |v3|^2)) Затем угол θ можно найти, применив функцию арккосинуса: θ = arccos(cos(θ)) Вот подробное решение: 1. Найдем векторы: v1 = B - A1 = (2 - 1, 4 - 2, 2 - 3) = (1, 2, -1) v2 = C - A = (3 - 1, 1 - 2, 3 - 3) = (2, -1, 0) v3 = D1 - A = (3 - 1, 4 - 2, 3 - 3) = (2, 2, 0) 2. Выполним скалярное произведение: s1 = v1 · v2 = (1 * 2) + (2 * -1) + (-1 * 0) = 2 - 2 + 0 = 0 s2 = v1 · v3 = (1 * 2) + (2 * 2) + (-1 * 0) = 2 + 4 + 0 = 6 3. Найдем длины векторов: |v1| = √(1^2 + 2^2 + (-1)^2) = √(1 + 4 + 1) = √6 |v2| = √(2^2 + (-1)^2 + 0^2) = √(4 + 1 + 0) = √5 |v3| = √(2^2 + 2^2 + 0^2) = √(4 + 4 + 0) = √8 = 2√2 4. Найдем угол: cos(θ) = (s1 + s2) / (|v1| * √(|v2|^2 + |v3|^2)) cos(θ) = (0 + 6) / (√6 * √(5 + 8)) cos(θ) = 6 / (√6 * √13) cos(θ) = 6 / (√78) θ = arccos(cos(θ)) θ = arccos(6 / (√78)) Полученное значение θ будет углом между прямой A1B и плоскостью ACD1. Необходимо учесть, что для вычисления конкретного численного значения этого угла потребуется использовать калькулятор или математическое программное обеспечение.