В коробке 8 деталей, из них 5 окрашенных. Вынимают 2 детали. Определить вероятность того , что обе детали оказались окрашенными.

Вероятность того, что обе детали оказались окрашенными — .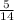

Пошаговое объяснение:

Вынимание первой детали:

Когда мы вынимаем первую деталь, в коробке у нас 5 окрашенных деталей из 8. Соответственно, вероятность вынуть окрашенную деталь —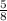 , так как:

Вероятность = число благоприятных исходов : число всех исходов

Что в итоге:

Если же мы вынули окрашенную деталь, то мы продолжаем вынимать, а в коробке осталось:

1) 8 - 1 = 7 ( д. ) — всего.

2) 5 - 1 = 4 ( д. ) — окрашенных.

Если же нет — то вынимать далее бессмысленно, так как надо, чтобы обе детали были окрашенными, а одна из них не окрашена.

Вынимание второй детали:

Когда мы вынимаем вторую деталь — вероятность того, что мы вынем окрашенную деталь равна , так как в коробке осталось уже 7 деталей, из них 4 — окрашены.

Рассчитаем вероятность:

Значит, вероятность вынуть 2 окрашенные детали равна:

3)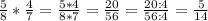 - вероятность того, что обе детали оказались окрашенными.

Здесь мы воспользовались правилом, которое гласит (я его переформулировал):

Вероятность происхождения двух событий равна вероятности происхождения первого события умноженной на вероятность происхождения второго события.

≈0,36

Пошаговое объяснение:

Количество благоприятных исходов: С₅²=10

Всего вариантов: С₈²=28

Р= С₅²/С₈²

 ≈0,36