В классе 24 человека. Из них 13 учеников посещают кружок по рисованию, 8 — кружок по математике, а пятеро не посещают ни один из этих кружков . Какова вероятность того ,что случайно выбранный ученик класса посещает кружок по математике, но не ходит на рисование.​

25%

Пошаговое объяснение:

Р=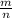, где м - благоприятные исходы, н - общее кол-во учеников

13+8+5=26. значит два ученика ходят и на матан, и на художку. Их откидываем.

остается 8-2=6 учеников

6/24=0.25=25%

Для решения данной задачи нам необходимо знать, сколько учеников посещает только кружок по математике и сколько учеников посещает оба кружка. Используя эти данные, мы сможем определить количество учеников, которые посещают только кружок по математике.

Из условия задачи мы знаем, что всего в классе 24 человека. Поэтому мы можем рассчитать количество учеников, которые посещают оба кружка. Для этого необходимо вычислить разность между количеством учеников, посещающих кружок по рисованию, и общим количеством учеников, посещающих оба кружка.

Количество учеников, посещающих оба кружка:
8 - (24 - 13 - 5) = 8 - 6 = 2

Итак, теперь мы знаем, что 2 ученика посещают оба кружка, а 6 учеников посещают только кружок по математике.

Теперь мы можем рассчитать вероятность того, что случайно выбранный ученик класса посещает кружок по математике, но не ходит на рисование.

Вероятность посещения кружка по математике, но не рисованию, можно выразить как отношение количества учеников, которые посещают только кружок по математике к общему числу учеников в классе:

Вероятность = (Количество учеников, которые посещают только кружок по математике) / (Общее количество учеников)

Вероятность = 6 / 24 = 1/4 = 0.25 = 25%

Итак, вероятность того, что случайно выбранный ученик класса посещает кружок по математике, но не ходит на рисование, равна 25%.