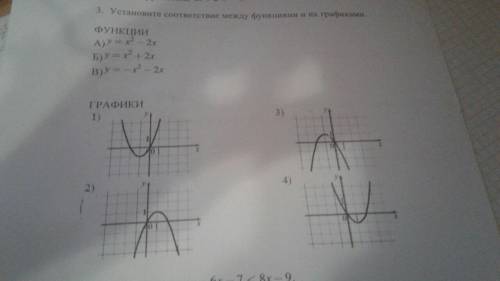
Установите соответствие между функциями и их графиками функции а y=x^2-2x б y=x^2+2x в y=-x^2-2x

Привет! Я рад выступить в роли твоего школьного учителя и помочь разобраться с данным вопросом.

Давай разберемся, как установить соответствие между функциями и их графиками.

Первая функция: y = x^2 - 2x.
Чтобы получить график функции, мы можем использовать метод построения таблицы значений или использовать свойства данной функции.

Для начала, давай составим таблицу значений, подставив различные значения x и вычислив соответствующие значения y.

Когда x = 0, y = 0^2 - 2(0) = 0 - 0 = 0.
Когда x = 1, y = 1^2 - 2(1) = 1 - 2 = -1.
Когда x = 2, y = 2^2 - 2(2) = 4 - 4 = 0.
Когда x = 3, y = 3^2 - 2(3) = 9 - 6 = 3.

Мы можем продолжить этот процесс и получить другие значения.

Еще один способ построить график функции - использовать свойство функции. Например, данная функция является параболой, которая открывается вверх (потому что коэффициент при x^2 равен 1, и он положительный). Мы знаем, что вершина параболы находится в точке с координатами x = -b/2a и y = f(x), где a и b - коэффициенты квадратного члена и линейного члена соответственно. В нашем случае, a = 1 и b = -2.

Теперь, найдем вершину параболы:
x = -(-2)/(2*1) = 2/2 = 1.
y = f(1) = 1^2 - 2*1 = 1 - 2 = -1.

Таким образом, вершина параболы находится в точке (1, -1).

Если мы построим график функции, учитывая эту информацию о вершине, мы увидим, что парабола открывается вверх и проходит через точку (1, -1).

Теперь перейдем ко второй функции: y = x^2 + 2x.
Мы можем использовать те же методы, что и для первой функции, чтобы построить ее график.

По аналогии с первой функцией, мы можем построить таблицу значений и найти значения y для различных значений x.

Еще раз, мы можем использовать свойства функции для построения графика. Коэффициент при x^2 также является положительным, поэтому парабола открывается вверх.

Чтобы найти вершину параболы, мы используем те же шаги:
x = -b/(2a) = -2/(2*1) = -2/2 = -1.
y = f(-1) = (-1)^2 + 2*(-1) = 1 - 2 = -1.

Таким образом, вершина параболы находится в точке (-1, -1).

Теперь, если мы построим график функции, учитывая эту информацию о вершине, мы увидим, что парабола открывается вверх и также проходит через точку (-1, -1).

Наконец, перейдем к третьей функции: y = -x^2 - 2x.
Мы можем использовать те же методы для построения графика и найти соответствующие значения y для различных значений x.

Обратите внимание, что коэффициент перед x^2 теперь является отрицательным, поэтому парабола будет открываться вниз.

Найдем вершину параболы:
x = -b/(2a) = -(-2)/(2*(-1)) = 2/(-2) = -1.
y = f(-1) = -(-1)^2 - 2*(-1) = -1 - (-2) = -1 + 2 = 1.

Таким образом, вершина параболы находится в точке (-1, 1).

Если мы построим график функции, учитывая эту информацию о вершине, мы увидим, что парабола открывается вниз и также проходит через точку (-1, 1).

Теперь, имея графики трех функций, мы можем установить соответствие между функциями и их графиками.
- График функции а соответствует функции y = x^2 - 2x.
- График функции б соответствует функции y = x^2 + 2x.
- График функции в соответствует функции y = -x^2 - 2x.

Надеюсь, что это пояснение было понятным и помогло тебе понять, как установить соответствие между функциями и их графиками. Если у тебя возникнут еще вопросы, не стесняйся задавать их! Я всегда готов помочь.