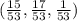Установить, что векторы a{- 3; 1; 7}, b{9; -1; 0},c{- 2; 2; 1} образуют базис, и найти координаты вектора d в этом базисе, если вектор d {2; 0; -2} .
Другие вопросы по теме Математика
Популярные вопросы
- Определить вид связи: 1. незаметно подкрасться 2. говорить по- 3. ничего не зная...
3 - Используя следующие пары слов и союзы (и , а, но, да, или) составьте и запишите...
2 - Дорога от дома до магазина у светы занимает 4 менуты что в 6 раз менше чем она...
1 - Высокие , средние и низкие голоса оперных певцов...
3 - Дядя миша пошёл в лес за ,но дождь застал его прямо у входа в лес. сколько грамматических...
2 - На складе 100 кг яблок, содержание воды в которых составляет 99%. при сушке содержание...
3 - Спроектом, надо. проект на тему жизненные стратегии современной молодёжи нужно...
1 - Меняется ли направление ускорение при прямолинейном движении?...
1 - Қасқырдың атынан тиінге хат жаз хатта тиінді қорқытпайтыныңды ашуланбайтіныңды...
2 - Сколько метров пробежит спортсмен со скоростью 8 метров в секунду за 4 секунды...
3
Пошаговое объяснение:
Базис - линейно независимая система. Так как матрица квадратная, то можно не преобразовывать ее по Гауссу, а просто посчитать детерминант.
Определитель не равен нулю, значит векторы линейно независимы, потому составляют базис.
Находим координаты вектора в базисе. Для этого нужно составить систему уравнений и записать ее в матрицу, где каждый вектор из базиса - столбик.
Итого, координаты вектора [2, 0, -2] в данном базисе будут