Упростите логическое выражение до трёх логических операций Варианты ответа:
а) ¬A+ B+C
б) ¬A+BC
в) A+¬B+C
г) A+ B+¬C
д) AB+¬C
е) ¬B+AC
ё) AB¬C
ж) ¬B+A¬C
з) ¬ABC
и) ¬BC+A
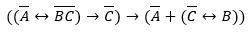
Другие вопросы по теме Математика
Популярные вопросы
- Кластер про Курмнгазы заранее за...
1 - Пуля массой 8 г движется со скоростью 800 м/с. Найдите скорость отдачи автомата...
2 - Задача.На висоті 400 метрів +23 градуса.Якою буде температура на висоті 1)200м...
3 - Решите химия 8 класс превращения ...
1 - какими красками Айши Гарифовна написала картину дастархан кр...
3 - диагонали четырёхугольника являются биссектрисами его углов докажите что в таком...
3 - Чинники Розміщення та Пояснення чинників розміщення: АЕС, ГЕС, ГАЕС, ТЕС, ТЕЦ,...
2 - Народ Нужно сделать сообщение по теме: СанПиН 2.1.3.2630-10 Санитарно-эпидемиологические...
3 - 1. Уявіть, що у вас є можливість зусрітися з героями повісті «Гобсек». Підготуйте...
3 - Лучник стреляет 20-граммовой стрелой со скоростью 40 м/с в 500-граммовую мишень....
3
1. Первая операция: A ∨ ¬B ∨ C. Здесь операция ∨ обозначает логическое ИЛИ. В данном случае, внутри скобок, у нас три переменные A, B и C, и каждая из них может быть истинной (1) или ложной (0).
2. Вторая операция: A ∧ B ∧ C. Здесь операция ∧ обозначает логическое И. Также, подобно предыдущей операции, внутри скобок, у нас три переменные A, B и C, и каждая из них может быть истинной или ложной.
3. Третья операция: ¬A. Здесь операция ¬ обозначает отрицание (НЕ). В данном случае, у нас есть одна переменная A, которая также может быть истинной или ложной.
Теперь мы можем сократить логическое выражение:
A ∨ ¬B ∨ C ∧ A ∧ B ∧ C ∧ ¬A
Для сокращения выражения, мы можем убрать переменные, которые встречаются в различных состояниях (истинные и ложные) внутри скобок. После использования этой логики, мы можем заметить, что переменные A и ¬A взаимно противоположны. То есть, если одна из них истинна, то другая ложна.
Исключая переменные, которые встречаются противоположными, наше выражение принимает следующий вид:
(A ∨ ¬B ∨ C) ∧ (B ∧ C)
Теперь, этот результат является более упрощенным выражением, которое содержит только три логические операции: две операции ИЛИ и одну операцию И.
Поэтому, правильный ответ на данный вопрос состоит в варианте ответа г) A+ B+¬C.