[умоляю! ] решите уравнение на фото!
Другие вопросы по теме Математика
Популярные вопросы
- Мальвина поставила на шахматную доску 8 на 8 клеток n шашек и велела буратино...
1 - Чехов после театра краткое содержание...
1 - Найти массу тела если известен угол 45 градусов...
2 - Из двух городов расстояние между которыми 220 км навстречу друг другу вышли...
3 - Визначити кути паралелограма, знаючи що один з них = 78°15...
2 - Решите уравнение 4^х+1-6^х=2*9^х+1...
3 - Оля связала плед длиной 2м6дм и шириной 1м9 дм. ленту какой длины взяла оля...
3 - Отгадай слово, объединяющее предложенные пары слов. магазин и пулемёт. река...
3 - Заполнить тест. заранее . 1. the bird is funny but the cat is … a) funny;...
3 - Нужно найти в этом тексте 4 предложения с временем present perfect. before...
2
x=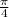 +
+ 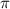 k , k∈Z
k , k∈Z
Пошаговое объяснение:
ОДЗ:
умножаем крест-накрест
степени взаимо сокращаются