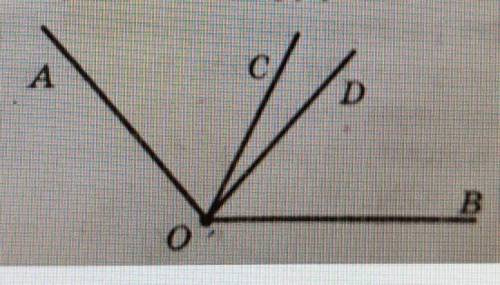
Угол АОВ равен 130". Луч ОС является его биссектрисой. Угол AOD на 30° больше угла DOB. Вы числите градусную меру угла COD.
​с решением если можно

Для решения данной задачи, нам понадобятся знания о биссектрисе угла и свойствах углов.

Из графика видно, что угол AOD является внутренним и суммируется с углом DOB, а их сумма равна углу COD.

Запишем данную информацию:

Угол AOD = Угол DOB + (30°)

Также, по определению биссектрисы, угол AOC разделяется лучом OS на два равных угла, то есть:

Угол AOC = Угол COB

Если мы присмотримся к треугольнику AOC, то можем заметить, что сумма всех углов в треугольнике равна 180°. Поэтому, мы можем записать следующее равенство:

Угол AOC + Угол COA + Угол OAC = 180°

Вспомним, что углы AOC и COA равны (по определению биссектрисы), поэтому их сумма будет равна два раза угол AOC:

2 * Угол AOC + Угол OAC = 180°

Теперь, применим все эти знания к решению задачи.

Из условия задачи известно, что угол АОВ равен 130°. Также, луч ОС является биссектрисой этого угла. Значит, угол AOC равен половине угла АОВ:

Угол AOC = 130° / 2 = 65°

Используя равенство, которое мы получили для треугольника AOC, найдем значение угла OAC:

2 * 65° + Угол OAC = 180°

Угол OAC = 180° - 2 * 65° = 50°

Теперь, вернемся к равенству, которое мы записали для углов AOD и DOB:

Угол AOD = Угол DOB + 30°

Угол AOD = 50° + 30° = 80°

Наконец, найдем значение угла COD, которое мы ищем. Мы знаем, что угол COD равен сумме углов AOD и DOB:

Угол COD = Угол AOD + Угол DOB

Угол COD = 80° + 50° = 130°

Таким образом, числовая мера угла COD равна 130°.