Ученик написал сочинение по теме «Треугольники». Вот некоторые фрагменты его сочинения 1. Треугольник – это геометрическая фигура, состоящая из трех точек, соединенных попарно отрезками.
2. Среди треугольников особенно выделяется равнобедренный треугольник. Если в нем провести любую биссектрису, она будет являться медианой и высотой.
3. Площадь любого треугольника можно вычислить по формулам:
S=1/2* ah и S= 1/2 ab* sinC
4. Если в треугольник вписана окружность, то его площадь можно найти по формуле S= abc/4R , где радиус этой окружности вычисляется по теореме косинусов: R= a/2cosA.
5. А если около треугольника описать окружность, то для нахождения площади
треугольника справедлива формула S = (a + b + c)*r .
6. Прямая, параллельная стороне треугольника, является его средней линией.
7. Существуют равные и подобные треугольники. Для доказательства равенства и подобия используют признаки. Например, треугольники равны, если углы одного соответственно равны углам другого. Кроме того, любые прямоугольные треугольники подобны.
Все ли верно в сочинении ученика? Напишите , ошибки и правильный вариант.
Другие вопросы по теме Математика
Популярные вопросы
- X - 2y ² + 2xy 1 x + 2y x2 – 4y2 (2y – x)2 (x + 2y)2 4y2...
2 - Вычислить значения выражениц: 587706+(213956-41916):34=?...
1 - Решите неравенство: х^2 (1 −х)/х^2−14х+49≤0...
2 - Сообщение характеристика Чехии 1945 год 1950 год политический строй...
3 - Выпишите из текста А предложение с обобщающим словом при однородных...
1 - «Московском государстве не было собственных золотых и серебряных...
2 - Заполните формулу попс на тему вклад абая в сокровищницу общенациональной...
3 - 3) Выпин строки, в которых рассказывается, как работают актеры кукольного...
1 - В чем заключалось принципиальное отличие международных договоров...
2 - Объективной необходимостью для поддержания жизнедеятельности и обеспечения...
1
1. Треугольник – это геометрическая фигура, состоящая из трех точек, соединенных попарно отрезками.
Приемлемо, однако следует добавить, что эти три точки не лежат на одной прямой.
2. Среди треугольников особенно выделяется равнобедренный треугольник. Если в нем провести любую биссектрису, она будет являться медианой и высотой.
Это неверно. И медианой, и высотой является только биссектрисса угла, противолежащего основанию, а не любая.
3. Площадь любого треугольника можно вычислить по формулам:
Верно.
4. Если в треугольник вписана окружность, то его площадь можно найти по формуле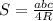 , где радиус этой окружности вычисляется по теореме косинусов:
, где радиус этой окружности вычисляется по теореме косинусов: 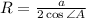 .
.
Неверно. Речь идет про описанную окружность, а не вписаную.
5. А если около треугольника описать окружность, то для нахождения площади треугольника справедлива формула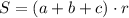
Здесь так же перепутаны вписанная и описанная окружности. Речь идет про вписанную окружности. К тому же ее радиус вычисляется по теореме синусов, а не косинусов.
6. Прямая, параллельная стороне треугольника, является его средней линией.
Неверно. Не всякая прямая, паралельная стороне треугольника является его средней линией. Можно дополнить тем, что прямая проходит через середину другой стороны, тогда это будет средняя линия.
7. Существуют равные и подобные треугольники. Для доказательства равенства и подобия используют признаки. Например, треугольники равны, если углы одного соответственно равны углам другого. Кроме того, любые прямоугольные треугольники подобны.
В тексте приведен признак подобия треугольников, но не равенства. Не все прямоугольные треугольники подобны. Для подобия двух прямоугольных треугольников достаточно чтобы были равны два острых угла.
Исправленный вариантТреугольник – это геометрическая фигура, состоящая из трех точек, соединенных попарно отрезками, не лежащими на одной прямой.
Среди треугольников особенно выделяется равнобедренный треугольник. Если в нем провести биссектрису угла, противолежащего основанию, она будет являться медианой и высотой.
Площадь любого треугольника можно вычислить по формулам:
Если около треугольника описана окружность, то его площадь можно найти по формуле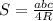 , где радиус этой окружности вычисляется по теореме синусов:
, где радиус этой окружности вычисляется по теореме синусов: 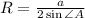
А если в треугольник вписать окружность, то для нахождения площади треугольника справедлива формула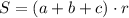 .
.
Прямая, параллельная стороне треугольника и проходящая через его середину, является его средней линией.
Существуют равные и подобные треугольники. Для доказательства равенства и подобия используют признаки. Например, треугольники подобны, если углы одного соответственно равны углам другого. Кроме того, любые прямоугольные треугольники с парой равных острых углов подобны.