Участвую в конкурсе по и не могу решить 1) дано уравнение а*b + a*b = вектор ab. условие : а и b имеют одинаковое количество цифер и они положительные. вектор аb
показывает число, если написать a и b друг за другом. например: вектор аb = 2019, если а = 20, b=19. нужно найти возможные числа для a и b
Другие вопросы по теме Математика
Популярные вопросы
- 6. вычислите периметр прямоугольника, еслиширина его равна 45 см,...
2 - На невесомой нерастяжимой нити висит шарик малой массы m. справа...
2 - Мне надо для школы ответить на некоторые вопросы только постарайтесь...
3 - Вычислите интеграл. желательно с решением...
1 - Напишите краткое содержание лермонтова песня про царя ивана васильевича...
3 - Решить уравнение sin(x)=cos³(x), достаточно свести его к кубическому...
1 - Какая главная мысль в произведении а.с.пушкина выстрел ?...
3 - Найти наибольший корень уравнения: 4log(6) ( 3-( 3/(2x+3) ) ) =...
3 - Решите два примера по информатике...
2 - Хсоставляет 50% от у , у больше ,чем z на 300% .на сколько процентов...
2
Пусть кол-во цифр а и b равно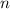
Тогда: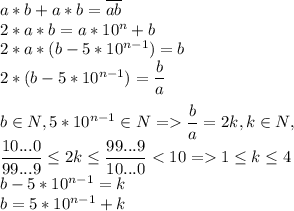
1)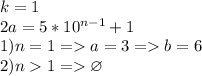
т.к. в случае 2. получаем равенство нечетного и четного чисел, что неверно.
2)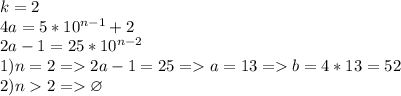
т.к. в случае 2. получаем равенство нечетного и четного чисел, что неверно.
3)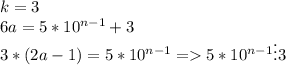 ,
,
что неверно.
4)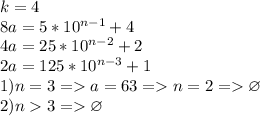
т.к. в случае 2. получаем равенство нечетного и четного чисел, что неверно.
ответ: (3; 6), (13, 52)