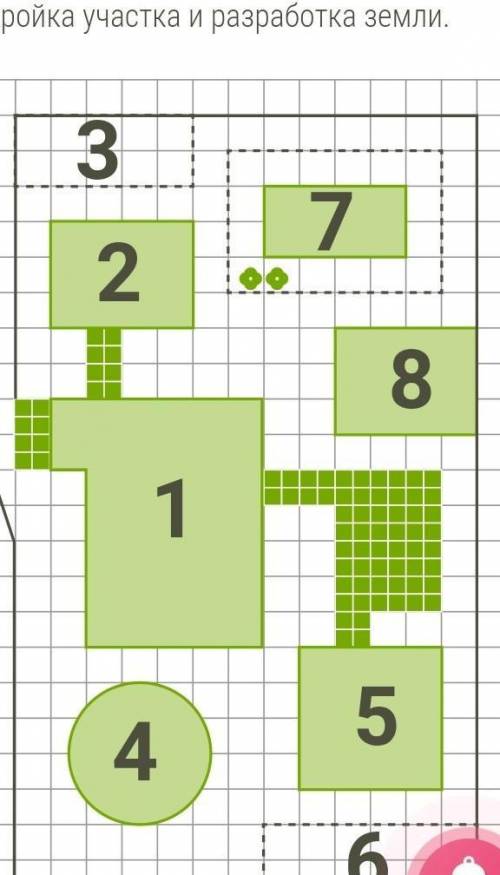
Участок имеет форму вытянутого прямоугольника, въезд и выезд через единственные ворота. От ворот можно попасть в дом по выложенному плиткой участку. Слева от ворот располагается курятник, справа — декоративная клумба с пряностями. Перед воротами выложена площадка из тротуарной плитки, ей же вымощены некоторые дорожки на участке. Гараж на схеме отмечен цифрой 8. Вокруг теплицы отведено место под разведение цветов. Баня на участке находится за домом, перед ней есть площадка. На участке есть электричество и центральный водопровод. Все площадки и дорожки на участке выложены одной и той же плиткой и в каждой клетке схемы помещается по 4 плитки, в соответствии со схемой. Размер стороны клетки на плане — 0,6 м. Рядом с теплицей высажены цветы. Дом обозначен цифрой 1. Сколько метров составит самое короткое расстояние от жилого дома до теплицы? ответ дай в метрах, при необходимости округли до десятых. В поле для ответа внеси только число, без единиц измерения и других дополнительных символов.

​

Это просто, я из-за баллов,

Для решения данной задачи, мы можем использовать геометрический подход и применить теорему Пифагора.

1. По схеме видно, что дом обозначен цифрой 1, а теплица - цифрой 6. Нам нужно найти самое короткое расстояние между этими двумя точками.

2. Размеры клетки на плане 0.6 м. Теплица находится на расстоянии 3 клеток от дома по горизонтали, и 4 клеток по вертикали. Обозначим эти расстояния как a и b соответственно.

3. Для нахождения самого короткого расстояния между домом и теплицей, нам нужно найти гипотенузу прямоугольного треугольника, где катеты равны a и b.

4. Используя теорему Пифагора, мы можем записать уравнение: гипотенуза^2 = a^2 + b^2.

5. Подставляя значения a = 3 и b = 4, получим: гипотенуза^2 = 3^2 + 4^2 = 9 + 16 = 25.

6. Чтобы найти гипотенузу, нужно извлечь квадратный корень из обеих сторон уравнения: гипотенуза = √25 = 5.

Таким образом, самое короткое расстояние от жилого дома до теплицы составит 5 метров.