у десятичной записи числа 2 в 2020 степени посчитали сумму цифр. У этой суммы снова посчитали сумму цифр и так далее, пока не осталась 1 цифра, какая?
Другие вопросы по теме Математика
Популярные вопросы
- Дан треугольник ABC такой, что ∠A=75°, ∠B=60°, AC=9√6см. Найди...
1 - Виконай дії 12/23-4/23+13/23...
3 - A) How many things do we compare in every sentence? b) Which...
3 - Написать сочинение -отзыв на рассказ Бунина Лапти по вопросам;1)Какое...
3 - написать сочинение на тему Февральский день...
3 - СОЧИНЕНИЕ НА ТЕМУ ЕВГЕНИЙ ОНЕГИН - ТИПИЧНЫЙ ПРЕДСТАВИТЕЛЬ СВОЕГО...
1 - Сообщение Основные грамматические нормы современного русского...
3 - Решить уравнения: 1) |x|=3,5; 2)|y|=0; 3)|x|=-4; 4) |x+5|=7....
1 - Перепишите, вставьте пропущенные буквы. Раскройте скобки. (Не)молодой...
1 - РЕШИТЕ НОМЕР 977 НОМЕР УМАЛЯЮ...
2
7
Пошаговое объяснение:
Вспомним признак делимости на 9: число делится на 9 тогда и только тогда, когда его сумма цифр делится на 9.
Этот признак работает и для равноостаточности при делении на 9. То есть, число и его сумма цифр имеют одинаковый остаток при делении на 9.
Пусть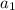 - изначальное число и
- изначальное число и 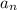 - сумма цифр числа
- сумма цифр числа 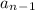 . Пусть остаток при делении на 9 у числа
. Пусть остаток при делении на 9 у числа 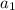 - r, тогда и у числа
- r, тогда и у числа 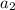 остаток при делении на 9 тоже r. Но тогда и у чисел
остаток при делении на 9 тоже r. Но тогда и у чисел 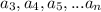 остаток при делении на 9 равен r. Но так как r - чисто от 0 до 9, то это и есть наша оставшаяся в конце цифра.
остаток при делении на 9 равен r. Но так как r - чисто от 0 до 9, то это и есть наша оставшаяся в конце цифра.
Тогда нам нужно всего лишь найти остаток при делении на 9 у числа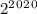 . А он такой же, как у числа
. А он такой же, как у числа 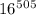 , и такой же, как у числа
, и такой же, как у числа 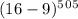 , и такой же, как у числа
, и такой же, как у числа 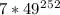 , а он такой же, как у числа
, а он такой же, как у числа 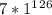 , а это равно 7.
, а это равно 7.