У=1/1-х^2 исследоват функции
Популярные вопросы
- (2,5х-7)*(2х+3)+3х+4=(4х-9)*(1,5х+1)...
3 - Найти, пользуясь дополнительной ) сподвижников александра невского, участвовавших...
1 - Перевести с на без переводчика! 40 ! 1) рекомендуем вам ознакомиться с правилами...
2 - Y(x)=x в квадрате-3х+2 ф(х)=4х в квадрате-5х+1...
2 - Перечислите через запятую фамилии трёх персонажей пьес гоголя, чьи имена и отчества...
2 - Синоним жəне антоним болатын тұрақты сөз тіркестер керек ....
1 - От данных глаголов образуйте действительные и страдательные причастия времени.запишите...
3 - Помгите ! составте вопрос к предложению: ақын шабыт беретін қаламдарына ерекше мен...
2 - Война за независимость.создание сша. 1.причина и участники 2.дата образования сша...
3 - Известно что толщина лобной кости у стегоценоса (растительноядный динозавр) достигла...
2
Если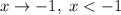 , то
, то 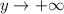 ; если
; если 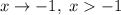 , то
, то 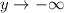
Если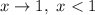 , то
, то 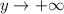 ; если
; если 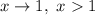 , то
, то 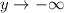
Найдем наклонные асимптоты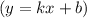 :
:
Если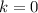 , то имеем горизонтальную асимптоту. Найдем
, то имеем горизонтальную асимптоту. Найдем 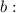
Следовательно,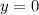 — горизонтальная асимптота.
— горизонтальная асимптота.
Из уравнения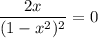 имеем критическую точку функции:
имеем критическую точку функции: 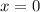
Заполним таблицу №1 (см. вложение).
Если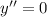 , то
, то 
Систематизируем данные, полученные по второй производной, в таблице №2 (см. вложение).
Для достоверности изобразим полученный график (см. вложение).