Тригонометрия 10 класс sinx=4/3; cosx=5/3√2; tgx=1/2; ctgx=5

Пошаговое объяснение:

По определению функции sinx для любого x∈(-∞; +∞): sinx∈[-1; 1]. Так как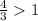 , то уравнение  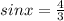 не имеет решений.

По определению функции cosx для любого x∈(-∞; +∞): cosx∈[-1; 1]. Так как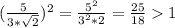 , следовательно 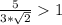, то уравнение  cosx= 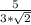не имеет решений.

Уравнение tgx=a имеет решения x=arctgx+π·k, k∈Z, поэтому из уравнения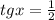 получаем решения x=arctg1/2+π·k, k∈Z.

Уравнение ctgx=a имеет решения x=arcctgx+π·k, k∈Z, поэтому из уравнения ctgx=5 получаем решения x=arcctg5+π·k, k∈Z.