Три насоса, работая вместе, заполняют бассейн за 5 часов. Известно, что первый насос накачивает в бассейн 30 литров воды за такое же время, за. которое второй накачивает туда 40 литров, а третий 90 литров воды. Сколько часов заполнялся бассейн, если первые два часа работали только первый и
третий насосы, третий и четвертый час – все три насоса, а начиная с пятого часа и до заполнения бассейна – работал только второй насос?
Другие вопросы по теме Математика
Популярные вопросы
- Установіть послідовність подій французької революції кінця 18століття...
3 - Якими були взаємини між руським та візантійським правителями?...
1 - 1. Тело переместилось из начальной точки с координатами х0 = -2м и у0...
1 - Какую часть развернутого угла составляет угол дусная мера которого равна...
1 - Сделайте предложения отрицательными, вписав m not, isn t, aren 1. You...
2 - Основна думка балади світязь текс даю 10 речень...
3 - Обчисліть масову частку солі в розчині, отриманому додаванням води масою...
1 - Як класифікуються українські балади? Наведіть приклад....
1 - Частота вращения диска 100 Гц, определите линейную и угловую скорости,...
3 - Как понять противоположенное качество ? так если оно противоположеное...
3
Обозначим время накачки t
Тогда первый насос прокачивает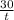 воды
воды
Второй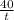
Третий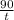
Вместимость бассейна =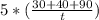 =
= 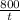
Составим уравнение:
Таким образом, бассейн заполнялся 2+2+6=10 часов
1) По условию первый насос накачивает в бассейн 30 литров воды за такое же время, за которое второй накачивает туда 40 литров, а третий 90 литров воды.
Обозначим это время х (часов), тогда
2)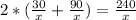 (л) объём воды, который поступил в бассейн за первые 2 часа.
(л) объём воды, который поступил в бассейн за первые 2 часа.
3)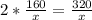 (л) объём воды, который поступил в бассейн за следующие 2 часа.
(л) объём воды, который поступил в бассейн за следующие 2 часа.
4)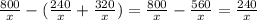 (л) объём воды, который через 2-й насос до заполнения бассейна.
(л) объём воды, который через 2-й насос до заполнения бассейна.
5)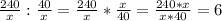 часов работала 2-я труба до заполнения бассейна.
часов работала 2-я труба до заполнения бассейна.
6)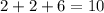 часов заполнялся бассейн.
часов заполнялся бассейн.
ответ: 10 ч.