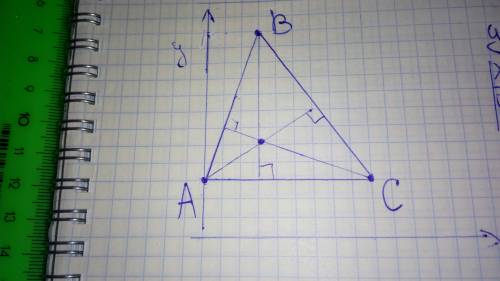
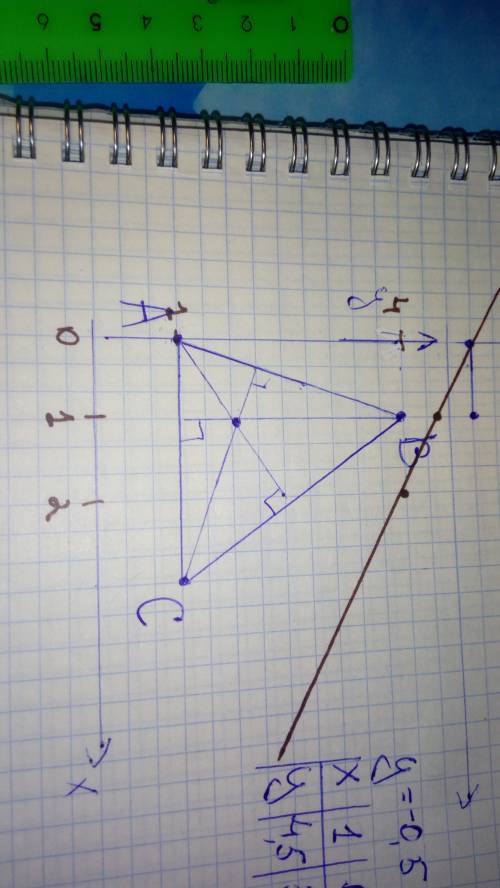
Треугольник задан вершинами а (0; 1) , в (1; 4) , с (3; 1) уравнение прямой, проходящей через точку пересечения его высот параллельно прямо y = -0,5x+5, имеет вид y = kx+b. найти значение k и b. , !
Ответы
Итак. 1).Начертили треугольник, провели высоты. 2). Нашли координаты точек прямой. На самом деле, достаточно найти 2 точки, чтоб построить прямую. 3). Построили эту прямую. 4). Нашли координаты точки пересечения высот: (.)О, это видно по графику четко. Нашли угловой коэффициент прямой, которая проходит через точку пересечения высот и параллельна y = -0,5x + 5. 5). Наполовину уравнение второй прямой готово: y2 = -0,5x. Надо найти свободный коэффициент, то есть, точку пересечения с осью ОУ. Подставляем значения (.)О в уравнение. Отсюда выражаем свободный коэффициент b. Находим коэффициент. 6). Уравнение готово: y2 = -0,5x + 2,16.



ПОКАЗАТЬ ОТВЕТЫ





Другие вопросы по теме Математика
Популярные вопросы
- 1) найдите функцию,обратную к данной : у= 2/х-3 ( / - дробная черта) у= х3...
2 - Вокружности длиной 36п проведена хорда, стягивающая дугу в 60 градусов. найдите...
1 - Определить тему,тип и стиль речи текста.выделеть ключевые слова помню, бродили...
2 - Функции-прямая,параллельная оси абсцисс проходящая через точку м(5,8).задайте...
2 - Вычислите 1.tg(-390*)2.cos(-11п/4) 1.sin(180*-a)-cos в квадрате (180*+а)/cos(a-270*)2.sin105*cos15*sin15*sin165*tg225*...
1 - Где пишется втайне слитно а где раздельно ? (пример)...
2 - :преобразовать в многочлен 1)2ab x (2a степень2-5ab+ b степ2) 2) -3ab x (2a...
2 - Из каких 2 предлогов можно составить название животного? а из 3 предлогов?...
1 - Из следующих высказываний выберите,те в которых говорится о элементе и те...
1 - Напишите характеристику деда каширина горький детсво 1портрет 2речь героя...
3