Треугольник ABC задан координатами вершин: A(−4;−2), B(−2;4), C(4;2). Определи вид треугольника ABC по его сторонам и найди его площадь

Ответы

annaozerkevich 03.02.2022 17:33

Δ АВС- равнобедренный,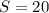 S=20 кв. ед.

Пошаговое объяснение:

Найдем стороны треугольника, воспользовавшись формулой расстояния между точками

$d= \sqrt{(x{_1}- x{_2})^{2}+(y{_1}-y{_2})^{2} }$

$A(-4;-2); B(-2;4) \\AB=\sqrt{(-4+2) ^{2}+(-2-4) ^{2} } =\sqrt{(-2)^{2} +(-6)^{2} } =\sqrt{4+36} =\sqrt{40}=2\sqrt{10} ;$

$A(-4;-2); C(4;2)\\AC= \sqrt{(-4-4) ^{2} +(-2-2)^{2} } =\sqrt{(-8)^{2} +(-4)^{2} } =\sqrt{64+16} =\sqrt{80} =4\sqrt{5} ;$

$B(-2;4); C( 4;2) \\BC= \sqrt{(-2-4)^{2} +(4-2) ^{2} } =\sqrt{(-6)^{2} +2^{2} } =\sqrt{36+4} =\sqrt{40} =2\sqrt{10} .$

Так как AB=BC , то Δ АВС - равнобедренный.

Проведем высоту ВМ, в равнобедренном треугольнике она является и медианой.

Значит, АМ= МС= 4√5: 2=2√5 ед.

Рассмотрим прямоугольный треугольник Δ АМВ и найдем катет ВМ по теореме Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.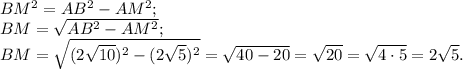 $BM^{2} =AB^{2} -AM^{2} ;\\BM = \sqrt{AB^{2} -AM^{2} } ;\\BM= \sqrt{(2\sqrt{10})^{2} - (2\sqrt{5})^{2} } =\sqrt{40-20} =\sqrt{20} =\sqrt{4\cdot5} =2\sqrt{5} .$