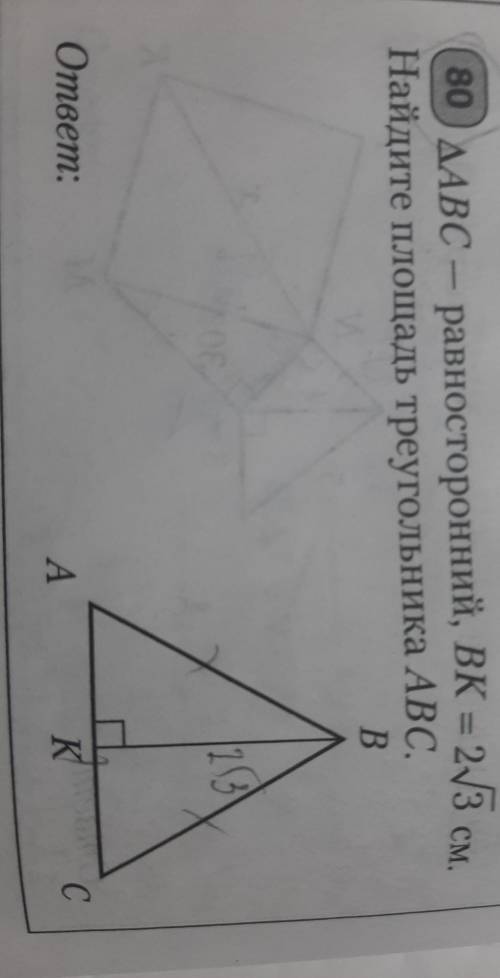
Треугольник abc - равносторонний , Bk=2 корень 3 см
Найдите площадь треугольника ABC.​

Чтобы найти площадь треугольника ABC, нужно использовать формулу для площади равностороннего треугольника:

\[S = \frac{a^2\sqrt{3}}{4}\]

где S - площадь треугольника, а - длина стороны треугольника.

Дано, что Bk = 2 корень 3 см.

Так как треугольник ABC - равносторонний, значит, все его стороны равны. Поэтому можно сказать, что Bk = 2 корень 3 см равно длине любой стороны треугольника, включая сторону BC.

Таким образом, сторона BC равна 2 корень 3 см.

Также, поскольку треугольник ABC - равносторонний, все его углы равны 60 градусов.

Теперь мы можем использовать формулу для площади треугольника:

\[S = \frac{a^2\sqrt{3}}{4}\]

Так как треугольник ABC - равносторонний, мы можем использовать длину любой стороны, чтобы найти площадь.

Давайте возьмем сторону AB. Так как треугольник равносторонний, сторона AB также равна 2 корень 3 см.

Теперь мы можем подставить эти значения в формулу для площади:

\[S = \frac{(2\sqrt{3})^2\sqrt{3}}{4}\]

\[S = \frac{12\sqrt{3}}{4}\]

\[S = 3\sqrt{3}\]

Таким образом, площадь треугольника ABC равна 3 корень 3 квадратных см.