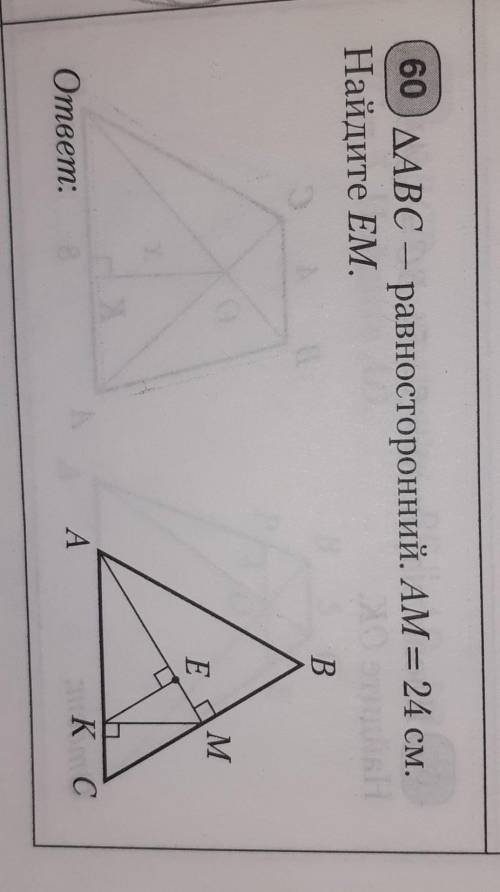
Треугольник ABC равносторонний AM равно 24 см найдите EM​

На рисунке дано, что треугольник ABC является равносторонним. Это означает, что все его стороны имеют одинаковую длину, то есть AB = BC = AC.

Также на рисунке дано, что отрезок AM имеет длину 24 см.

Нам нужно найти длину отрезка EM.

Для решения этой задачи воспользуемся свойствами равностороннего треугольника.

Свойство 1: В равностороннем треугольнике высоты, медианы и биссектрисы совпадают.

Это означает, что AM является не только медианой, но и высотой и биссектрисой треугольника ABC.

Свойство 2: Медиана делит сторону треугольника на две равные части.

Используя свойство 2, мы можем сказать, что AM делит сторону BC на две равные части. Поэтому BM = MC.

Теперь давайте найдем длину отрезка EM. Для этого мы можем воспользоваться теоремой Пифагора.

В правильном треугольнике ABC, AM является высотой, а BM является половиной стороны BC. Поэтому мы можем применить теорему Пифагора для нахождения длины отрезка EM.

Теорема Пифагора гласит: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин двух катетов.

В нашем случае, гипотенуза - это AM, а катеты - это BM и EM.

Таким образом, мы можем записать уравнение:
AM^2 = BM^2 + EM^2

Подставляя известные значения, получаем:
24^2 = (BM)^2 + (EM)^2

576 = (BM)^2 + (EM)^2

Мы уже знаем, что BM = MC, так как треугольник ABC равносторонний. Поэтому можем записать:
576 = (BM)^2 + (BM)^2

576 = 2(BM)^2

(БМ)^2 = 576 / 2

(БМ)^2 = 288

BM = √288

BM = 16.97 см (округляем до сотых)

Теперь нам нужно найти EM.

EM = BM = 16.97 см

Таким образом, длина отрезка EM равна 16.97 см.