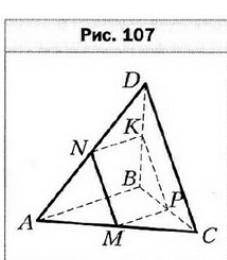
Точки М, N, К и Р — середины рёбер АС, AD, BD и ВС тетраэдра DABC соответственно, АВ = 30 см, CD = 26 см (рис. 107). Докажите, что точки М, N, К и Р являются вершинами параллелограмма, и вычислите периметр этого параллелограмма

Чтобы доказать, что точки М, N, К и Р являются вершинами параллелограмма, мы должны показать, что противоположные стороны параллелограмма равны и параллельны.

Вспомним, что середина отрезка делит его на две равные половины. Таким образом, М — середина отрезка АС, а N — середина отрезка АD. Из этого следует, что М и N делят отрезок АС пополам, и поэтому МС = МА и SN = NA.

То же самое верно и для отрезка ВС и его середины К и Р. Точка К является серединой отрезка BD, поэтому КВ = КД. Точка Р является серединой отрезка ВС, поэтому РВ = РС.

Теперь, чтобы доказать, что стороны МN и КР параллельны, мы можем воспользоваться свойством параллельных линий. Если две линии пересекаются с третьей линией так, что углы, образованные этими пересекающимися линиями, равны между собой, то эти две линии параллельны.

На рисунке видно, что М и Н лежат на отрезке АС, а К и Р лежат на отрезке ВD. Поэтому у нас есть два треугольника (МСН и КРВ), и углы, образованные этими треугольниками при точках С и В соответственно, равны между собой.

Таким образом, мы доказали, что стороны МN и КР параллельны.

Теперь докажем, что стороны МК и НР равны друг другу.
Мы знаем, что М — середина отрезка АС, а К — середина отрезка BD. Следовательно, МК делит отрезок BD пополам, и МК = КД.

Аналогично, Р — середина отрезка ВС, а Н — середина отрезка АD. Значит, РН делит отрезок AD пополам, и РН = NA.

Таким образом, стороны МК и НР равны друг другу.

Теперь мы можем вычислить периметр этого параллелограмма. Периметр параллелограмма вычисляется по формуле Р = 2(МК + МН). У нас уже есть, что МК = КД и МН = АС. Значит, периметр будет равен Р = 2(КД + АС).

По условию мы знаем, что АВ = 30 см и CD = 26 см. Так как точки М и N являются серединами соответствующих сторон, то АС = 2MN и КД = 2MN.

Итак, периметр будет равен Р = 2(КД + АС) = 2(2MN + 2MN) = 8MN.

Таким образом, периметр параллелограмма равен 8 разам длине отрезка МN. Для вычисления периметра мы должны знать длину отрезка МN. Однако в условии задачи эта информация не предоставлена, поэтому без дополнительных данных мы не можем вычислить точное значение периметра параллелограмма.