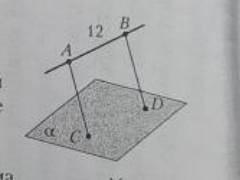
Точки C и D принадлежат плоскости альфа, AB параллельна BD, AB =12. Найдите расстояние между точками C и

Для решения этой задачи, нам понадобятся некоторые знания о геометрии и алгебре. Давайте пошагово разберемся, как решить эту задачу.

1. В изначальной информации сказано, что точки C и D принадлежат плоскости альфа, и AB параллельна BD, при этом AB = 12. Это означает, что отрезок AB имеет такую же длину, как и отрезок BD.

2. Известно, что отрезок AB = 12. Мы можем использовать это знание, чтобы найти длину отрезка BD. Так как AB и BD параллельны и имеют одинаковую длину, то BD также равняется 12.

3. Теперь у нас есть два отрезка: AC и CD. Мы должны найти расстояние между точками C и D. Для этого нам потребуется использовать теорему Пифагора.

4. Так как AC и BD параллельны и AB = BD, то мы можем сделать вывод, что треугольники ABC и BDC равны по двум сторонам и углу между ними. Поэтому угол B в обоих треугольниках равен 90 градусов.

5. Теперь мы можем применить теорему Пифагора к треугольнику BDC, чтобы найти длину отрезка CD. По теореме Пифагора, квадрат длины гипотенузы равен сумме квадратов длин катетов. В данном случае, катетом является отрезок BC равный 12, и гипотенузой является отрезок CD.

(CD)^2 = (BC)^2 + (BD)^2

(CD)^2 = 12^2 + 12^2

(CD)^2 = 144 + 144

(CD)^2 = 288

CD = √288

6. Для нахождения значения √288, мы можем применить традиционные методы вычислений или использовать калькулятор. Значение √288 примерно равно 16.97 (округлим до двух знаков после запятой).

CD ≈ 16.97

Таким образом, расстояние между точками C и D равно примерно 16.97.