Точка О - центр правильного двенадцатиугольника А1А2...А12. Найдите длину диагонали А1А5, если площадь треугольника А5ОА9 равна 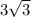. с подробным решением !

Чтобы найти длину диагонали А1А5 в правильном двенадцатиугольнике, нам нужно использовать некоторые геометрические свойства.

1. Найдем площадь треугольника А5ОА9. Мы знаем, что площадь треугольника равна (1/2) * основание * высоту. В данном случае, основание треугольника А5ОА9 равно А5А9, и площадь равна √3 (корень из 3). Таким образом, получаем:

(1/2) * А5А9 * высота = √3

2. Найдем высоту треугольника А5ОА9. Высота является перпендикуляром, опущенным из вершины треугольника к его основанию. Заметим, что треугольник А5ОА9 является равнобедренным треугольником, так как его стороны А5О и А5А9 равны (поскольку О - центр правильного двенадцатиугольника).

Таким образом, высота треугольника А5ОА9 является медианой и медиана делит ее основание пополам. Обозначим середину стороны А5А9 как точку В.

Тогда, А5В = ВА9 = А5А9 / 2.

3. Найдем длину стороны А5А9. Чтобы это сделать, мы можем разделить двенадцатиугольник на 12 равных правильных треугольников и использовать теорему Пифагора для прямоугольного треугольника А1А5А9.

В равностороннем треугольнике, сторона равна a и высота, опущенная к основанию, равна √(3/2) * a.

Теперь мы знаем, что сторона правильного двенадцатиугольника равна а (вопрос вводит А1А2...А12 как правильный двенадцатиугольник).

А5А9 = 2 * А1А5 = 2 * а

4. Подставим полученные значения в уравнение площади треугольника:

(1/2) * 2 * а * (√(3/2) * а / 2) = √3

5. Упростим выражение и решим уравнение:

а^2 * (√(3/2) / 2) = √3

а^2 = (√3 * 2 * 2) / (√3 / 2) = 4

а = 2

Таким образом, сторона правильного двенадцатиугольника А1А2...А12 равна 2.

6. Теперь найдем длину диагонали А1А5. Для этого воспользуемся теоремой Пифагора для треугольника А1А5О:

А1А5^2 = А1О^2 + ОА5^2

ОА5 (высота треугольника А5ОА9) равна (√(3/2) * а / 2) = √(3/2)

Таким образом,

А1А5^2 = 2^2 + (√(3/2))^2 = 4 + 3/2 = 11/2

А1А5 = √(11/2)

Таким образом, длина диагонали А1А5 равна √(11/2).