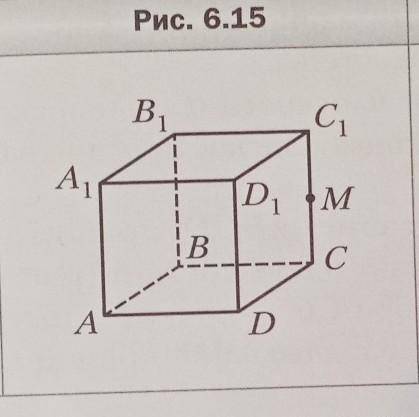
Точка М- середина сечения Сс1 КУБА ABCDA1B1BC1D1. Постройте сечение куба плоскостью, проходящей через точку М и параллельной плоскости A1BC. Найдите периметр полученного сечения, если ребро куба равно а.
Другие вопросы по теме Математика
Популярные вопросы
- яка кількість теплоти потрібна щоб розплавити кусок міді масою 10 кг взятий...
1 - Визначити константу, ступінь гідролізу солі в розчині та константу дисоціації...
1 - Раскройте скобки, употребляя требующуюся форму прилагательного : 1.The...
3 - Портрет мороза в сказке Снегурочка Островского...
3 - Указать над именами существительными падеж после смерти сасаки ребята...
3 - Який вигляд відносно Землі має траєкторія руху молекули?...
2 - Чим Скрудж пропонував до нужденним? Різдвяна пісня в прозі...
3 - Task 1. Write complete sentences. Use the present simple or the present...
3 - ала девочка. свои ощущения. Включите фразеологизмы и средства художественной...
1 - 3.Решите уравнения 1) x: 9 1/6=3 3/4 2) (1-7/10) x=2 1/4...
2
Поскольку точка М является серединой сечения Сс1, она делит отрезок Сс1 на две равные части. При этом отрезок Сс1 является диагональю грани куба ABCD.
1. Найдем длину диагонали грани куба ABCD.
Так как ребро куба равно а, длина диагонали грани равна √(а^2 + а^2) = √2а.
2. Найдем координаты точки М.
Точка М является серединой сечения Сс1, поэтому ее координаты будут равны средним координат точек C и с1.
Координата x:
x = (Cx + c1x) / 2 = (0 + а) / 2 = а / 2.
Координата y:
y = (Cy + c1y) / 2 = (0 + а) / 2 = а / 2.
Координата z:
z = (Cz + c1z) / 2 = а / 2.
Таким образом, координаты точки М будут (а / 2, а / 2, а / 2).
3. Построим плоскость, параллельную плоскости A1BC и проходящую через точку М.
Вспомним, что плоскость A1BC определяется точками A1, B, и C. Так как плоскость, которую нам нужно построить, параллельна плоскости A1BC, она будет иметь такие же направляющие векторы.
Направляющие векторы плоскости A1BC:
AC: (-a, 0, a)
A1B: (a/2, -a/2, a/2)
Таким образом, уравнение плоскости, параллельной плоскости A1BC и проходящей через точку М, будет иметь вид:
(ax - a/2)(-a) + (y - a/2)(-a/2) + (z - a/2)(a/2) = 0
-ax + a^2/2 - ay/2 + a^2/4 + az/2 - a^2/4 + az/4 - a^2/4 + az/4 - a^2/4 = 0
-a^2x/2 - ay/2 + a^2/4 + az/2 - a^2/4 + az/4 - a^2/4 + az/4 - a^2/4 = 0
-a^2x/2 - ay/2 + az/2 + a^2/4 - a^2/4 - a^2/4 - a^2/4 = 0
-a^2x/2 - ay/2 + az/2 - a^2/2 = 0
которое можно записать в виде:
-a^2x/2 - ay/2 + az/2 = a^2/2
4. Найдем периметр полученного сечения.
Для этого нам нужно найти длины сторон многоугольника, образующего сечение куба плоскостью, проходящей через точку М и параллельной плоскости A1BC.
Чтобы найти длину стороны многоугольника, необходимо найти расстояние между соответствующими точками на сечении куба.
Из предыдущего шага, у нас есть уравнение плоскости:
-a^2x/2 - ay/2 + az/2 = a^2/2
Заменим x, y и z координаты соответствующими координатами на сечении.
x = а / 2
y = а / 2
z = а / 2
Подставим:
- (a^2/2)(a/2) - (a/2)(a/2) + (a/2)(a/2) = a^2 /2
Заметим, что все члены обратились в ноль. Это означает, что все точки сечения находятся на одной оси, а значит, сечение представляет собой линию.
То есть, сечение куба плоскостью, проходящей через точку М и параллельной плоскости A1BC, является точкой М.
В таком случае, периметр этого сечения равен нулю.