1. Математика
  2. Точка м делит гипотенузу

Точка м делит гипотенузу ас прямоугольного треугольника авс в отношении ам: мс=2: 3. найдите разложение вектора вм по векторам ва и вс и длину вектора вм, если ав=10 см, св=5 см.

МиланаЖиза МиланаЖиза    3   03.09.2019 18:00    39

Ответы
katasinicina39 katasinicina39  06.10.2020 15:21

Из условия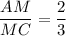 \dfrac{AM}{MC}=\dfrac{2}{3}, тогда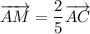 \overrightarrow{AM}=\dfrac{2}{5}\overrightarrow{AC}

По правилу треугольника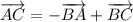 \overrightarrow{AC}=-\overrightarrow{BA}+\overrightarrow{BC}

Далее снова по правилу треугольника ABM:

\overrightarrow{BM}=-\overrightarrow{BA}+\overrightarrow{AM}=-\overrightarrow{BA}+\dfrac{2}{5}\overrightarrow{AC}=-\overrightarrow{BA}+\dfrac{2}{5}\overrightarrow{BC}-\dfrac{2}{5}\overrightarrow{BA}=\dfrac{2}{5}\overrightarrow{BC}-\dfrac{7}{5}\overrightarrow{BA}

Поскольку векторы BA и BC перпендикулярны, то их скалярное произведение равно нулю, следовательно,

\left|\overrightarrow{BM}\right|=\sqrt{\left(\dfrac{2}{5}\overrightarrow{BC}-\dfrac{7}{5}\overrightarrow{BA}\right)^2}=\sqrt{\dfrac{4}{25}BC^2+\dfrac{49}{25}BA^2}=\sqrt{4+196}=10\sqrt{2}~_{\sf CM}


Точка м делит гипотенузу ас прямоугольного треугольника авс в отношении ам: мс=2: 3. найдите разложе
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
CloudSmile CloudSmile  09.03.2021 21:21
а)7/18+1/9 вычислите б) 1/2-3/8 вычислите c)1/21-9/14 вычислите д) 5/42 -8/21+1/14 вычислите е) 13/24:26/33+5/12 вычислите ф)7/15-2/3*5/6...
123123324322221 123123324322221  09.03.2021 21:22
1 5 Б А Л Л О В ! ! ! -3(5x-7)=12,9...
Еденорожка666 Еденорожка666  09.03.2021 21:22
(-3 9/20) + 5 3/4 - значок / это дробь ответьте...
  09.03.2021 21:22
1) 2,2. (x-4); 2) -2. (1,2n - m)3)(4c-d) ×(-0, 5y) 4) (6×(p+0, 3k-1, 2t) Быстрее ​...
Sanpotion Sanpotion  09.03.2021 21:23
по кругу отметили 15 точек и каждую соединили отрезком ровно с четырьмя другими. сколько проведено отрезков...
umeson umeson  09.03.2021 21:23
Из генеральной совокупности извлечена выборка, которая пред- ставлена в виде интервального вариационного ряда (см. таблицу): а) пред- полагая, что генеральная совокупность...
Янаvi Янаvi  09.03.2021 21:23
сколько 5 нужно чтобы вчетверти была 5 в четверти если текущие ТОЛЬКО ЧЕСТНО И ПРАВИЛЬНОЕСЛИ ДО КОНЦА ЧЕТВЕРТИ ОСТАЛОСЬ 3 УРОКА ДАМ ЕСЛИ ЧЕСТНО ❗❗❗❗...
Ральфф Ральфф  09.03.2021 21:25
- 1 х + 4х – 8x = -9,9; 0,6y - 1,9у - 0,5y = 0,54;12 15- x - - x + - х = -8 3 2 187-9-b+2=b+1 — b=19 62 36 4 12 27• Виконайте дії:-84 : 2,1 - 4,64 :(-5,8) - 6:24 + 1,4...
meribageee meribageee  25.05.2020 19:00
Найди значение выражения 5⋅x−3⋅(7⋅x+3) при x=7.​...
Zopa43 Zopa43  24.05.2020 18:59
Производная её применение y=x^2/x^3-9 с абсциссой x^0=-1...

Популярные вопросы