Точка брошена наугад в круг x^2+y^2 =1. какова вероятность того, что расстояние от точки до центра превысит 0.5

Question

Математика: Точка брошена наугад в круг x^2+y^2 =1. какова вероятность того, что расстояние от точки до центра превысит 0.5

alinahan444 · Answer

x² + y² ≤ 1 — окружность с центром (0;0) и радиусом R = 1, область которой лежит внутри окружности.

Расстояние от точки до центра окружности превысит 0.5, если эта точка не попадет в окружность с центром (0;0) и r = 0.5

Площадь большей окружности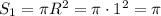 $S_1=\pi R^2=\pi \cdot 1^2=\pi$

Площадь меньшей окружности: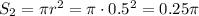 $S_2=\pi r^2=\pi\cdot0.5^2=0.25\pi$

Разность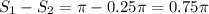 $S_1-S_2=\pi-0.25\pi=0.75\pi$

Вероятность того, что расстояние от точки до центра превысит 0,5, равна (по формуле геометрической вероятности):

$P=\dfrac{S_1-S_2}{S_1}=\dfrac{0.75\pi}{\pi}=0.75$

ответ: 0,75.

Точка брошена наугад в круг x^2+y^2< =1. какова вероятность того, что расстояние от точки до центра превысит 0.5