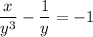; y(0)=1)
найти частно решение
Другие вопросы по теме Математика
Популярные вопросы
- :4 предложения по татарскому языку про друга...
2 - 48 больших ёлочных шариков упаковали поровну в 4 одинаковые коробки и а 4 такие...
3 - Найдите отрезки отсекаемые прямой 5x-y+20=0 на осях координат...
1 - Втрёх шкафах 600 книг во 2 шкафу на 50 книг больше чем в 1 а в 3 на 50 книг больше...
3 - На основе текста 22 составьте и запишите три предложения с обобщающими словами...
2 - Найдите точку пересечения прямых x-y+8=0 и 2x+5y-4=0...
1 - Инайдите значение выражения 902 икс минус 833 икс плюс 1001 минус 966 если x равняется...
2 - На завод поступило 77 деталей. их решили разделить между 3 рабочий. первый получил...
1 - Конькобежец пробежал на стадионе 5 кругов радиусом в 100 м. определить пройденный...
2 - Три пятых всего участка занимает фруктовый сад. какова площадь всего участка,...
3
Данное дифференциальное уравнение перепишем в следующем виде
где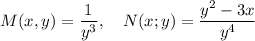
Тогда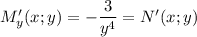 , что собственно можем сделать вывод, что данное диф. уравнение является уравнением в полных дифференциалах
, что собственно можем сделать вывод, что данное диф. уравнение является уравнением в полных дифференциалах
Если функция F(x;y) удовлетворяет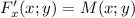 и
и 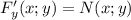 , то
, то 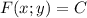 - решение дифференциального уравнения
- решение дифференциального уравнения
Интегрируем по переменной х
далее продифференцируем по переменной у
Откуда общий интеграл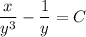
Найдем частный интеграл, подставляя начальные условия
Частный интеграл: