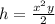![\sqrt{2}*\sqrt[3]{2}*\sqrt[6]{2}](/tex.php?f=\sqrt{2}*\sqrt[3]{2}*\sqrt[6]{2})
решить уравнение:

из формулы выразить переменную h:

Другие вопросы по теме Математика
Популярные вопросы
- Найдите и исправьте ошибку (ошибки) в образовании формы слова. запишите...
3 - Втечении 5 секунд магнитный поток проходящий через проволочный контур...
3 - Диаметр круга 10см.чему равен его радиус...
3 - Вырази в секундах 15 мин,8мин,45с,105мин,2ч,6ч 10 мин,1 ч 20 мин 10 сек...
1 - 30б.характеристика семьи болконских ( война и мир ) 1) члены семейства...
3 - Сочинение встреча с старым знакомым...
1 - Пяточку нужно разрезать ленточку длинной 124 см на две части так, чтобы...
2 - (0,39+9,42+3,41): 3=; (6,07+12,41+2,011): 3; вычеслите среднее арифмическое...
2 - Исследовать функцию и построить график 1) y = 2 - 3x^2 - x^3 2) y= x/x+1...
3 - Решите уравнение 5\7x = 6 целых 3\7. с полным ходом решения...
3
Пошаговое объяснение:
ответ: 2.
ОДЗ: х > 0.
x ∈ (0; 3)
ответ: x ∈ (0; 3).
ответ: