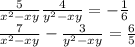
Другие вопросы по теме Математика
Популярные вопросы
- 9x^4+6x^2b+b^2-9=подробное решение...
3 - Определите объем бетонной плиты, если в пресной воде на нее действует...
2 - Укажите правильное определение.Вводные слова – это слово или сочетание...
1 - решите систему неравенств{5х+7≤0,2х+6 0;...
2 - |3-4x|+|-y| При x=2,1 и y=0,4 Решение и ответ...
2 - Карточка1. Вставь, где надо, ь знак.Уличный, пузыр...ки, дочка, скуч...ный,...
3 - Обчислити суму перших 9 членів арифметичної прогресії (an), якщо дані...
3 - Отношение к любви русалки в сказке Андерсона...
2 - Гіпотегуза прямокутного трикутника дорівнює13 см а один із катетів 12см....
1 - с заданием до всьо на картинке...
2
(5; 3) и (-5; -3)
Пошаговое объяснение:
Т.к. (-3)²=3², (-5)²=5² и -3×(-5)=3×5, то подходит и решение (-5; -3).
Решение в файле. Там же иииии ответ.)