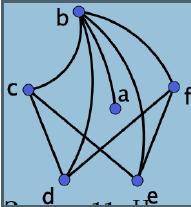
Теория вероятности 7 класс Задача 10. а) Сколько вершин у графа, изображённого слева?
б) А сколько в нём рёбер?
в) Какова степень вершины f в этом графе?
г) Какая вершина имеет наибольшую степень?
д) Какая вершина имеет наименьшую степень?
е) Нарисуйте этот граф так, чтобы его рёбра не пересекались.
Другие вопросы по теме Математика
Популярные вопросы
- Для засолки огурцов готовят 6 процентный россол. приготовить 40 г такого раствора...
1 - 3).преобразуйте выражение в одночлен стандартного вида: a) -6а3b7∙5a2 ∙b )3....
3 - Составьте программу, которая заполняет массив a[1..15] случайными целыми числами...
2 - Make the sentence negative 1 my dad works in a hotel. 2 my friends like sport...
1 - У= 0.5 х - 3 с таблицей и графиком. желательно с обьяснениями....
3 - Какая пословица выражает идею сказки о царе салтане ? сколько веревочке ни виться,а...
2 - Составить предложения со словами доплыть добежать прадед правнук попросить поиграть...
3 - )) complete the text with is or has got. anton student at school in voronezh....
3 - M+cl2=mcl2 рассмотрите реакцию в виде овр(степени окисления указывать не нужно)...
3 - Абонент сотовой связи выбрал тариф по которому ежедневно cо счёта снимает 0,5...
3
б) Чтобы выяснить количество ребер в графе, нужно посчитать количество линий, соединяющих вершины. На графе изображено 9 линий, соединяющих точки или узлы, значит, количество ребер в данном графе равно 9.
в) Степень вершины - это количество ребер, соединяющих эту вершину с другими вершинами графа. Для определения степени вершины f, нужно посчитать количество линий, исходящих из этой вершины или соединяющих ее с другими вершинами. В данном графе у вершины f 3 выходящих линии, значит, степень вершины f равна 3.
г) Чтобы определить, какая вершина имеет наибольшую степень, нужно посчитать степени всех вершин графа и найти максимальную из них. В данном графе все вершины имеют одинаковую степень 3, поэтому нет вершины с наибольшей степенью.
д) Для определения вершины с наименьшей степенью, нужно снова посчитать степени всех вершин графа и найти минимальную из них. В данном графе также все вершины имеют одинаковую степень 3, поэтому нет вершины с наименьшей степенью.
е) Чтобы нарисовать граф так, чтобы его ребра не пересекались, нужно поместить вершины и соединения между ними таким образом, чтобы линии не пересекались. Приведенный на картинке граф уже нарисован таким образом, что его ребра не пересекаются.
Надеюсь, ответы были понятны и полезны. Если у вас возникнут еще вопросы, не стесняйтесь задавать их.