1. Математика
  2. Теория вероятностей рабочий

Теория вероятностей

рабочий обслуживает 3 станка. вероятность того, что в течение смены его внимания потребует первый станок, равна 0,7, второй — 0.75, третий — 0.8.
найти вероятность того, что в течение смены внимания рабочего потребует не менее двух станков.

ANiTEZ ANiTEZ    3   06.08.2019 09:26    7

Ответы
meimanby meimanby  04.10.2020 00:49

Пусть случайная величина X - количество обслуживания станков, которые в течение смены потребуют внимания рабочего.

Из условия нужно подсчитать вероятность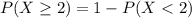 P(X\geq 2)=1-P(X

НО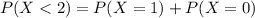 P(X

Вероятность того, что в течении смены внимания рабочего потребует один из станков равна

P(X=1)=(1-0.7)\cdot 0.75\cdot 0.8+0.7\cdot (1-0.75)\cdot 0.8+0.7\cdot 0.75\cdot (1-0.8)=\\ \\ =0.425

Вероятность того, что в течении смены станки не потребуют внимания рабочего, равна

P(X=0)=(1-0.7)\cdot (1-0.75)\cdot (1-0.8)=0.015

искомая вероятность: P(X\geq 2)=1-(0.425+0.015)=0.56

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
ekateria1411 ekateria1411  31.01.2021 14:38
Выпишите числа от 1 до 100 (в строке по 6 чисел) 1 2 3 4 5 6 7 8 9 10 11 12 и т.д....
FenomeN1703 FenomeN1703  31.01.2021 14:34
Решите мне задачу мама заготовила 18 литрав сока у нее получилось 5 одинаковых банок яблочного сока и 4 таких-же вижнового скок литрав сочка в 1 банке скок литров яблокчного...
Zubu Zubu  31.01.2021 14:34
Найдите площадь прямоугольника, сторона которого равна 6, а диоганаль 10.​...
yarrik00yaroslavchik yarrik00yaroslavchik  31.01.2021 14:34
Математика упражнение 467 6 класс...
nezandenzar nezandenzar  31.01.2021 14:34
Площа ділянки 10 соток. Для побудови будинку відведено 2,5 соток. Скільки відсотків площі ділянки можна відвели для побудови будинку?​...
ANGEL7777771 ANGEL7777771  31.01.2021 14:34
Обчисліть швидкість автомобілю який за 24 хвилини проіхав 35 км...
Aldiyar26 Aldiyar26  31.01.2021 14:34
три ученика писали одно сочинение первый ученик написал 20% всего сочинение количество написанных слов вторым учеником третьим относятся как 2:3 3 ученик написала на 24 слов...
RuslAN3017 RuslAN3017  31.01.2021 14:33
с показательным неравенством(0,5)^2x-1 (0,25)^3x+4...
Sofia2224 Sofia2224  31.01.2021 14:33
Округлить число 16,6106 до десятых...
Niki567890 Niki567890  31.01.2021 14:33
(-15) плюс(-2 7/10) пример по матиматеке 6 класс...

Популярные вопросы