Тема первый признак подобия треугольников
решите задачи 1,2,3
Другие вопросы по теме Математика
Популярные вопросы
- Почему все авторы летописей заканчивали изложение событий началом XVIII...
2 - (7) Методи створення нових сортів рослин розробляє наука:а) біотехнологіяб)...
1 - А теперь вспомним сказку Н. Телешова «Белая цапля». В ней говорится о...
2 - Только можете оформить как надо) Во время гидролиза трипептида массой...
1 - У клітинку D2 введено формулу =IF(C2 0;B2+C2;B2-C2). Що буде результатом...
3 - Розкрити дужки, поставивши інфінітив у безособовій формі. 1. У хаті не(сидіти)....
2 - Для якої природної зони характерні тварини: слон, тигровий пітон, бенгальський...
3 - Что случилось с Митрашей на болоте??...
2 - Установите соответствие между формулой вещества и классом соединения:...
3 - Чим відрізнявся птах Джонатан Лівінгстон від інших птахів...
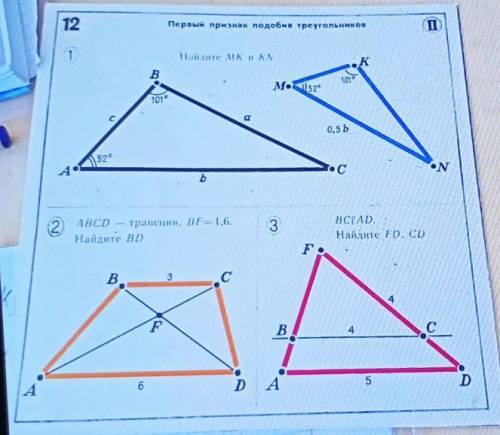
3
2) BD = 1,6 + 2 * 1,6 = 4,8
3) не понятно куда относится 4.
Задача 1:
В треугольнике ABC проведена высота CD. Докажите, что треугольник ABC подобен треугольнику CBD и найдите отношение их сторон.
Решение:
Для доказательства подобия треугольников ABC и CBD нам нужно проверить выполнение двух условий:
1. Угол BAC равен углу BDC (по условию задачи, в треугольнике ABC проведена высота CD).
2. Отношение длин сторон AB и BC равно отношению длин сторон CB и BD.
Первое условие: Угол BAC равен углу BDC.
В треугольнике ABC проведена высота CD, значит, угол BAC является прямым углом. Также, по свойству высоты треугольника, угол CBD тоже является прямым углом. Таким образом, углы BAC и BDC равны друг другу, и первое условие выполняется.
Второе условие: Отношение длин сторон AB и BC равно отношению длин сторон CB и BD.
Мы знаем, что высота CD является перпендикуляром к основанию AB. Значит, сторона CD является высотой треугольника ABC.
Также, по теореме Пифагора, мы можем найти длину стороны CB:
CB^2 = AB^2 - AC^2
CB^2 = 9^2 - 6^2
CB^2 = 81 - 36
CB^2 = 45
CB = √45
CB = 3√5
Теперь мы можем сравнить отношение сторон треугольников ABC и CBD:
AB/CB = 9/3√5
AB/CB = 3/√5 * 9/3
AB/CB = 3√5/√5 * 3
AB/CB = 9/3
AB/CB = 3/1
Таким образом, отношение длин сторон AB и BC равно отношению длин сторон CB и BD, и второе условие выполняется.
Таким образом, мы доказали, что треугольник ABC подобен треугольнику CBD по признаку подобия треугольников и отношение их сторон равно 3/1.
Теперь перейдем к задаче номер 2:
Задача 2:
В треугольнике ABC проведена медиана CE. Докажите, что треугольник ACE подобен треугольнику BCD и найдите отношение их сторон.
Решение:
Для доказательства подобия треугольников ACE и BCD нам нужно проверить выполнение двух условий:
1. Угол ACE равен углу BCD (по условию задачи, в треугольнике ABC проведена медиана CE).
2. Отношение длин сторон AE и EC равно отношению длин сторон BC и CD.
1. Угол ACE равен углу BCD.
В треугольнике ABC проведена медиана CE, значит, точка E делит сторону AB пополам. Таким образом, AE равна EB. Также, по свойству медианы треугольника, точка E делит сторону AC пополам. Таким образом, угол ACE равен углу AEC, и угол AEC равен углу BCD. Таким образом, первое условие выполняется.
2. Отношение длин сторон AE и EC равно отношению длин сторон BC и CD.
Мы знаем, что точка E делит сторону AB пополам, поэтому AE = EB. Аналогично, точка E делит сторону AC пополам, поэтому CE = EA.
Таким образом, отношение длин сторон AE и EC равно 1:1.
Теперь мы можем сравнить отношение сторон треугольников ACE и BCD:
AE/BC = 1/1
Таким образом, отношение длин сторон AE и EC равно отношению длин сторон BC и CD, и второе условие выполняется.
Таким образом, мы доказали, что треугольник ACE подобен треугольнику BCD по признаку подобия треугольников и отношение их сторон равно 1/1.
И, наконец, перейдем к задаче номер 3:
Задача 3:
В треугольнике ABC проведена биссектриса AD. Докажите, что треугольник ABD подобен треугольнику ACD и найдите отношение их сторон.
Решение:
Для доказательства подобия треугольников ABD и ACD нам нужно проверить выполнение двух условий:
1. Угол BAD равен углу CAD (по условию задачи, в треугольнике ABC проведена биссектриса AD).
2. Отношение длин сторон AB и BD равно отношению длин сторон AC и CD.
1. Угол BAD равен углу CAD.
В треугольнике ABC проведена биссектриса AD, значит, точка D делит угол BAC пополам. Таким образом, угол BAD равен углу DAC. Также, по свойству биссектрисы треугольника, отрезок BD делит стороны треугольника ABC пропорционально. То есть, отношение длин сторон AB и BD равно отношению длин сторон AC и CD. Таким образом, первое условие выполняется.
2. Отношение длин сторон AB и BD равно отношению длин сторон AC и CD.
Мы знаем, что отрезок BD делит сторону AC пропорционально, поэтому
AB/BD = AC/CD
Теперь мы можем рассмотреть другое отношение длин сторон треугольников ABD и ACD:
AB/AC = BD/CD
Мы можем сравнить эти два отношения:
AB/BD = AB/AC
Таким образом, отношение длин сторон AB и BD равно отношению длин сторон AC и CD, и второе условие выполняется.
Таким образом, мы доказали, что треугольник ABD подобен треугольнику ACD по признаку подобия треугольников и отношение их сторон равно AB/BD = AB/AC.
Я надеюсь, что данное пошаговое решение помогло вам понять процесс доказательства и решения задач по признаку подобия треугольников. Если у вас возникнут еще вопросы или нужна дополнительная помощь, не стесняйтесь обращаться ко мне.