Тема: "Модуль"

114.
Прямая проходит через точки A (2; 3) и B (12;-2). Есть ли у этой прямой точка:
а) С (-14; 11)
б) D (165; –78)?​

уравнение прямой, проходящей через две точки

(х-х₁)/(х-х₂)=(у-у₁)/(у-у₂)

а) (х-2)/(12-2)=(у-3)/(-2-3)

(х-2)/(10)=(у-3)/(-5); х-2=-2*(у-3);х-2=-2у+6;  2у=6+2-х; у=4-х/2

С(-14;11)

подставим ее координаты в уравнение прямой у=4-х/2

11=4+14/2; 11=11, верно. да. точка С(-14;11) принадлежит прямой у=4-х/2

б)  D (165; –78)

подставим ее координаты в уравнение прямой у=4-х/2

-78=4+165/2; нет. точка D (165; –78) не  принадлежит прямой у=4-х/2, т.к. справа дробное число, а слева целое

Прямая, которая задается уравнением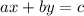 , можно переписать в виде функции 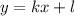, где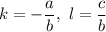

Определим формулу линейной функции, которая проходит через две точк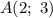и: и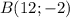

Для этого подставим соответствующие координаты точек в функцию и получим систему из двух линейных уравнений:

Из первого уравнения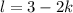 подставим во второе уравнение:

Тогда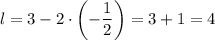

Получили линейную функцию, которая задается формулой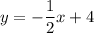

Для проверки того, проходит ли прямая через заданную точку, следует подставить координаты этой точки в функцию и посмотреть результат.

а) Для точки :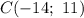

— правда

б) Для точки :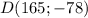

— неправда

ответ: а) да; б) нет.