Тема Линейное неравенство с одной переменной и их решение. Двойное неравенство.
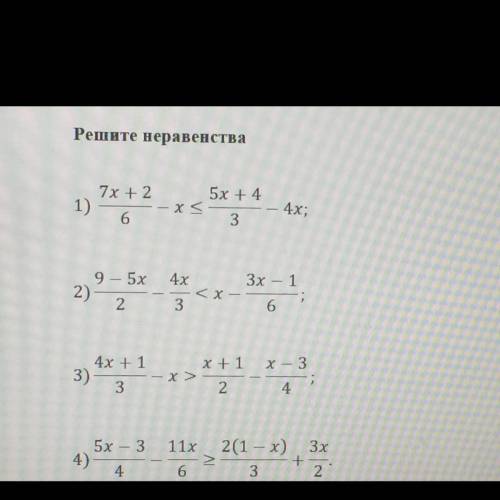
Решите неравенства
7х + 2
1)
5х + 4
х<
3
4x;
6
9 - 5x
2)
4х
3
3х - 1
6
2
I
4х +1
3)
3
х+1
x >
2
x – 3
4
5х – 3
4)
4
11x 2(1 - x) 3x
2
+
6
3 2
100%
Текст для поиска
12:22
Другие вопросы по теме Математика
Популярные вопросы
- Перевидите dolls collecting is easy and fun...
3 - Основные виды наркотических веществ, находящихся в незаконном...
1 - Как решить ? а) х\2=16 б) x\2=0 в) x\2=26 г) х\2=-9 с действиями...
3 - Составить предложение на со словом который. одно....
2 - Пятнистую кошку скрестили с рыжим котом. как пойдет разчепление...
1 - Весной зелена, лето загорела, осенью надела красные кораллы...
1 - Площадь равностороннего треугольника равна 4√3 см^2.найти радиус...
3 - Какие государства говорят на славянских языках?...
2 - За что выступает справедливая ответьте. желательно быстро и понятно....
1 - Кратко но точно (21,5 ×(36,8-27,4)+6,8×(12,7+))×10...
3
В решении.
Пошаговое объяснение:
1) Переписывать не буду, сразу решение:
Умножить все части неравенства на 6, чтобы избавиться от дробного выражения:
7х + 2 - 6х <= 2(5х + 4) - 24х
х + 2 <= 10х + 8 - 24х
х + 2 <= 8 - 14x
x + 14x <= 8 - 2
15x <= 6
x <= 6/15
x <= 0,4
Решение неравенства: х∈(-∞; 0,4]
Неравенство нестрогое, скобка квадратная, а знак бесконечности всегда с круглой скобкой.
2) Умножить все части неравенства на 6, чтобы избавиться от дробного выражения:
3(9 - 5х) - 2*4х < 6*x - 3x + 1
27 - 15x - 8x < 6x - 3x + 1
27 - 23x < 3x + 1
-23x - 3x < 1 - 27
-26x < -26
26x > 26 (знак неравенства меняется при делении на -1)
x > 1
Решение неравенства: х∈(1; +∞).
Неравенство строгое, скобка круглая, а знак бесконечности всегда с круглой скобкой.
3) Умножить все части неравенства на 12, чтобы избавиться от дробного выражения:
4(4x + 1) - 12x > 6(x + 1) - 3(x - 3)
16x + 4 - 12x > 6x + 6 - 3x + 9
4x + 4 > 3x + 15
4x - 3x > 15 - 4
x > 11
Решение неравенства: х∈(11; +∞).
Неравенство строгое, скобка круглая, а знак бесконечности всегда с круглой скобкой.
4) Умножить все части неравенства на 12, чтобы избавиться от дробного выражения:
3(5x - 3) - 2*11x >= 4*2(1 - x) + 6*3x
15x - 9 - 22x >= 8 - 8x + 18x
-7x - 9 >= 8 + 10x
-7x - 10x >= 8 + 9
-17x >= 17
17x <= -17
x <= -1
Решение неравенства: х∈(-∞; -1].
Неравенство нестрогое, скобка квадратная, а знак бесконечности всегда с круглой скобкой.