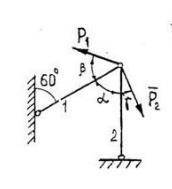
Техническая механика, определение реакции в жестких стержнях P1=8
P2=5
Углы
α=60
β=60
y=45

Добрый день! Сегодня мы рассмотрим определение реакции в жестких стержнях с помощью технической механики. У нас есть изображение стержней с указанными значениями сил и углов. Давайте начнем.

Первое, что нам нужно сделать, это разбить силы на горизонтальные и вертикальные компоненты. Найдем горизонтальные и вертикальные силы P1 и P2.

Горизонтальная составляющая силы P1 равна:
P1x = P1 * cos(α)
P1x = 8 * cos(60)
P1x = 8 * 0.5
P1x = 4

Вертикальная составляющая силы P1 равна:
P1y = P1 * sin(α)
P1y = 8 * sin(60)
P1y = 8 * 0.866
P1y = 6.928

Горизонтальная составляющая силы P2 равна:
P2x = P2 * cos(β)
P2x = 5 * cos(60)
P2x = 5 * 0.5
P2x = 2.5

Вертикальная составляющая силы P2 равна:
P2y = P2 * sin(β)
P2y = 5 * sin(60)
P2y = 5 * 0.866
P2y = 4.33

Теперь мы можем рассчитать реакцию опоры в точке A. Поскольку стержни жесткие, то реакция в точке A может быть только вертикальной.

Согласно принципу равновесия по вертикали, сумма вертикальных сил должна равняться нулю. У нас есть сила P1y, направленная вниз, и реакция опоры в точке A, направленная вверх. Таким образом, можно записать уравнение:

R_A - P1y + P2y = 0,

где R_A - реакция опоры в точке A.

Подставляя известные значения, получаем:

R_A - 6.928 + 4.33 = 0,

R_A = 6.928 - 4.33,
R_A = 2.598.

Таким образом, реакция опоры в точке A равна 2.598 единицам силы.

Теперь перейдем к рассмотрению реакции опоры в точке B. Так как у нас нет горизонтальных сил в этой точке, мы рассмотрим только вертикальные силы.

Сумма вертикальных сил также должна быть равна нулю. У нас есть реакция опоры в точке B, направленная вверх, и вертикальная составляющая силы P1, направленная вниз. Уравнение будет выглядеть следующим образом:

R_B + P1y = 0,

где R_B - реакция опоры в точке B.

Подставляя известные значения, получаем:

R_B + 6.928 = 0,

R_B = -6.928.

Таким образом, реакция опоры в точке B равна -6.928 единицам силы.

Надеюсь, я смог пояснить и разобрать эту задачу достаточно подробно. Если есть еще вопросы, пожалуйста, не стесняйтесь задавать.