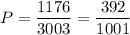Іте решіть у ящику у довільному порядку розкладені 15 деталей, причому 7 з них сиандартні. робітник бере 5 деталей. знайти імовірність того, що два з них будуть стандартні
Другие вопросы по теме Математика
Популярные вопросы
- Установите, являются ли приведенные рассуждения логически правильными. Если философ...
2 - іть бистріше 2 3 4 Завдання потрібно...
2 - Если умер Перикл, то он умер или когда жил, или когда умер. Если когда жил, то...
2 - пж помогите решить кр пж быстрее ____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________-------------------------------___________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________...
1 - Представьте себя в роли дипломата к. XVI- XVII вв. Вам необходимо составить докладную...
2 - желательно кратко объяснить...
3 - Задание 2. Используя Венн диаграмму, сравните уровни развития Англии, России,...
3 - 6 - тапсырма . Мәтінге сүйеніп , ұнататын театрын туралы шағын мәтін құра . Онда...
2 - Нужно заполнить таблицу в скрине...
2 - Степь чем далее, тем становилась прекраснее. Тогда весь юг, все то пространство,...
2
ответ: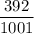 .
.
Пошаговое объяснение:
Общее число возможных элементарных исходов равно числу которыми можно извлечь 5 детали из 15
Подсчитаем число исходов, благоприятствующих данному событию:
Для этого нужно посчитать сколькими среди выбранных 5 деталей выбрать 2 стандартных, при этом из 15 деталей 7 стандартных .
Всего таких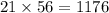 .
.
Вероятность того, что среди выбранных 5 деталей будут 2 стандартные детали: