Таблица 9.7 решение треугольников

Добрый день, ученик! Сегодня я с удовольствием ответю на твой вопрос о таблице 9.7 по решению треугольников.

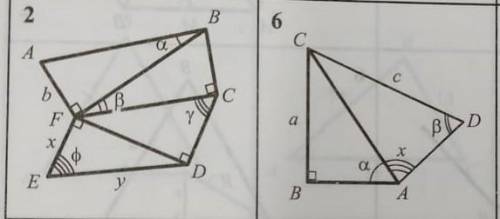
В таблице, которую ты привел, представлено решение треугольников, основанное на теореме синусов и теореме косинусов. Теорема синусов гласит:

В треугольнике со сторонами a, b и c и противолежащими углами A, B и C соответственно верно, что:

a / sin A = b / sin B = c / sin C (1)

где sin A означает синус угла A. Данная теорема позволяет нам связать отношения сторон и углов в треугольнике.

Теорема косинусов гласит:

В треугольнике со сторонами a, b и c и углом A противолежащим стороне a верно, что:

c^2 = a^2 + b^2 - 2ab * cos A (2)

где cos A означает косинус угла A. Данная теорема позволяет нам находить значения сторон или углов, если известны другие значения.

Таблица, которую ты видишь, представляет различные комбинации известных и неизвестных значений в треугольнике. В первом столбце таблицы приведены различные комбинации известных сторон и углов. Во втором и третьем столбцах указаны формулы, которые используются для решения треугольников в каждой конкретной ситуации.

Давай посмотрим на пример решения треугольника с известными сторонами a, b и c. В таблице приведена формула для нахождения угла A:

A = arccos [(b^2 + c^2 - a^2) / (2bc)]

где arccos oзначает арккосинус. Чтобы решить треугольник, нужно подставить известные значения a, b и c в эту формулу и вычислить угол A. Аналогично, можно использовать формулы для нахождения углов B и C.

Также таблица предоставляет формулы для нахождения сторон треугольника, если известны стороны и углы. Например, если известны сторона a и углы B и C, можно использовать формулу:

b = a * (sin B / sin A)

где sin B и sin A - синусы углов B и A соответственно.

Ученик, я надеюсь, что данное объяснение помогло тебе понять таблицу 9.7 по решению треугольников. Эти формулы позволяют нам решать различные задачи, связанные с треугольниками, и находить неизвестные значения сторон или углов. Если у тебя есть вопросы или нужно дополнительное объяснение, я всегда готов помочь!

оророророророророрроррр