Существует ли прямоугольный треугольник длины сторон которого удовлетворяют соотношению a^2+b^2=5c^2? В ответ введите значение(a/c)^2. ЕСЛИ ОТВЕТОВ НЕСКОЛЬКО ВВЕДИТЕ ИХ ВСЕ!​

2

Пошаговое объяснение:

Пусть a,c - катеты. b - гипотенуза

Тогда по Т. Пифагора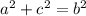

Получаем систему:

Подставляем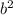 из первого уравнения во второе

============  

Не забывайте нажать " ", поставить оценку и, если ответ удовлетворил, то выберите его как "Лучший"  

Бодрого настроения и добра!  

Успехов в учебе!

Существует ли прямоугольный треугольник длины сторон которого удовлетворяют соотношению a²+b²=5c² ? В ответ введите значение(a/c)². ЕСЛИ ОТВЕТОВ НЕСКОЛЬКО ВВЕДИТЕ ИХ ВСЕ ​!

ответ:   2.                                            (a/c)²_ кв. отнош. катетов              

Очевидно с  не гипотенуза   (иначе a²+b²=c²) . с → катет. И пусть гипотенуза  b ( ∠B =90°)  , второй катет → a.

{  c² + a² = b²    ( теорема Пифагора );

{ 5c² - a² = b²   ( условие задачи ) .

Следовательно     с²+ a²= 5c² -а² ⇔ 2a²=4c² ⇔  (a/c)² =2.

Да,существует такой прямоугольный треугольник a/c =√2 ; tg∠A =√2 .

∠A =arctg(√2) .

1 < √2 < √3  ⇒   ∠A  ∈ ( 30° ; 60°)   ;          ∠A≈ 54° .