Существует ли многочлен p(x) с целыми коэффициентами такой, что p(0) =19; p(1) = 85; p(2) = 1985
Другие вопросы по теме Математика
Популярные вопросы
- Чем работа массажиста полезна обществу...
1 - Write the full verb form: 1. he for his girlfriend since 6 o clock....
3 - Ккакому виду относится сказка кот и лисат ...
3 - Сочинение по на тему плюсы и минусы рассказа человек в футляре...
2 - Найди значение выражения 62 013 : 3 +130*5=...
1 - Ширина прямоугольника равна 4 см это на а см меньше его длины...
1 - Михаил лермонтов — посреди небесных тел анализ...
3 - Лойко зобар как романтический герой из макар чудра и примеры....
3 - Вставь по порядку в стихотворение глаголы лежать, согреться, разбухнуть,...
3 - Сочинение описание моего настроения...
2
Существует
Пошаговое объяснение:
Попробуем предъявить такой многочлен. В точке 0 значение должно быть 19, так что многочлен должен иметь вид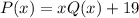 .
.
Подставляем x = 1: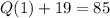 , тогда
, тогда 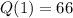 и
и 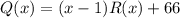 .
.
Подставляем найденное Q в P: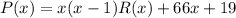
Теперь подставляем x = 2:
Самый простой удовлетворить такому требованию - взять R(x) = 917 тождественно, тогда получится полином
Можно получить и общий вид многочленов, удовлетворяющих условию. Для этого надо взять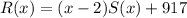 . Получим, что подойдут полиномы вида
. Получим, что подойдут полиномы вида
где многочлен S(x) можно выбрать произвольно