Существует ли 1000-значное число n, запись которого не содержит цифры 0, равное
сумме двух слагаемых, каждое из которых получается перестановкой цифр числа n.

Question

Математика: Существует ли 1000-значное число n, запись которого не содержит цифры 0, равное сумме двух слагаемых, каждое из которых получается перестановкой цифр числа n.

landeshforever · Answer

Чтобы найти такое число (если оно существует), достаточно найти такое k-значное число A (1000⋮k, чтобы число A можно было записать 1000/k раз и получить 1000-значное число), которое можно разбить на 2 k-значных слагаемых A₁ и A₂, образованных перестановкой цифр числа A. То есть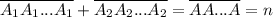 $\overline{A_1A_1...A_1}+\overline{A_2A_2...A_2}=\overline{AA...A}=n$ .

И действительно, такой пример можно подобрать: 1269 + 1692 = 2961. Значит, 12691269...1269 + 16921692...1692 = 29612961...2961 (каждое 4-значное число повторяется 250 раз). То есть такое число существует.

ответ: да

Существует ли 1000-значное число n, запись которого не содержит цифры 0, равное сумме двух слагаемых, каждое из которых получается перестановкой цифр числа n.

Популярные вопросы

Существует ли 1000-значное число n, запись которого не содержит цифры 0, равное
сумме двух слагаемых, каждое из которых получается перестановкой цифр числа n.