Сумма первых 24 членов арифметической прогрессии равна 33, а сумма первых 24 членов другой арифметической прогрессии, имеющей тот же первый член, но противоположную по знаку разность, равна (−8). Найти первые члены этих прогрессий.
Другие вопросы по теме Математика
Популярные вопросы
- 5 ;9841. Теңдеудің түбірлерін табыңдар:1) у = 9;3) y =2) |x| = 1,6;4)...
3 - Какие причины могут возникновению экстремизма и терроризма?...
1 - К раствору , содержащему 42,7г хлорида хрома (3 вал.) прилили раствор...
3 - Почему птенцы быстро покидают гнезда...
1 - У людини ген темного волосся домінує над світлим. Світловолоса жінка...
3 - Прочитайте внимательно текст о выдающемся ученом Алексея Александровича...
3 - Решение текстовых задач с уравнений. Урок 2 Смешали 2л 10%-го раствора...
3 - Тянь шань тауының тектоникалық құрылымы мен паидалы қазбалары...
2 - нажмите на фото чтоб развернуть....
3 - 2. Сұйықтар мен газдар неліктен қысымды барлық жаққа бірдей жеткізеді?...
2
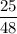
Пошаговое объяснение:Запишем - общий первый член,
- общий первый член, 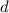 и
и 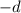 - разности прогрессий.
- разности прогрессий.
Запишем уравнения
Сложим оба уравнения