Сумма квадратов цифр некоторого положительного двузначного числа равна 25. Если от искомого двузначного числа отнять 9, то получится двузначное число, записанное теми же цифрами, но в обратном порядке.
Другие вопросы по теме Математика
Популярные вопросы
- 48 (корень из 5 минус 2) (корень из 5 плюс 2)...
3 - Слово свежей рыбой антоним ...
1 - Если сейчас апрель, то какое время года будет через 3 месяца?...
3 - Решите карточки . Желательно быстрее....
3 - Укажіть квадратне рівняння...
1 - Длина меньшего плеча рычага 30 см, большего 90 см. На большее плечо действует...
3 - Приведена таблица размеров одежды (пиджак и брюки) 20 восьмиклассников:...
2 - Найти прозводную функцииа)y =5y=5б)y =10xy=10xв)y =2x2+xy=2x2+xг)y =3x3y=3x3...
2 - До водного розчину етанолу об ємом 150 мл з масовою часткою спирту 96%...
1 - 4 сынып 5 есеп .Тенсиздиктерди окы.Кос тенсиздикти жеке екй тенсиздикке...
1
43
Пошаговое объяснение:
Пусть a, b — цифры двузначного числа. Тогда 10a+b — исходное число. По условию задачи составим систему:
Решим отдельно первое уравнение:
По теореме Виета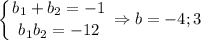
Цифра отрицательной быть не может, поэтому b = 3, a = 4. Исходное число — 43.