Сумма цифр трехзначного числа равна 8. последняя цифра обозначает число, которое больше числа, обозначающего предыдущую цифру, на число, которое обозначает первая цифра. назовите не менее двух вариантов таких чисел с решением

A₁=134; A₂=224; A₃=314; A₄=404

Пошаговое объяснение:

Пусть трёхзначное число A состоит из цифр x, y и z, то есть: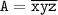 .  Так как x первая цифра трёхзначного числа, то x≥1.

По первому условию: x+y+z=8. По второму условию: z=y+x. Если последнее подставит в предыдущее уравнение, то получим:

x+y+(y+x)=8 ⇔ 2·(y+x)=8 ⇔ y+x=4 ⇒ z=y+x=4.

Отсюда следует, что мы должны рассматривать трёхзначные числа, в которых последняя цифра 4: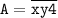 и y=4-x.

Перебираем все варианты первой цифры:

x=1 ⇒ y=4-1=3 ⇒ A₁=134;

x=2 ⇒ y=4-2=2 ⇒ A₂=224;

x=3 ⇒ y=4-3=1 ⇒ A₃=314;

x=4 ⇒ y=4-4=0 ⇒ A₄=404.

Вот и все варианты.