Сумма цифр двузначного числа равна 10. Если в этом числе переставить цифры, то оно уменьшится на 54. Найдите это число
Другие вопросы по теме Математика
Популярные вопросы
- Sometimes (mouse)___ are very smart....
1 - Напишите уравнения этантиола с гидроксидом калия...
3 - Чотири магазини деякого підприємця розташовано у вершинах опуклого чотирикутника....
3 - Мақал мәтелдерді қатыстырып, шетелдік досыңа туған жеріңді таныстыратын...
2 - Ақбілек шығармасындағы кейіпкерлерге мінездеме беріңіз. Кейіпкерлер бойындағы...
2 - Нужно решить вариант под буквой Б (7,3). Задача несложная. Решение у...
3 - Орфоэпический разбор слова заяц...
2 - При сгорании порции ненасыщенного углеводорода объёмом 44,8 дм³ (н. у.)...
3 - ответ по форме да/нет 1. Альфа Малой медведицы - это северный полюс мира?...
2 - 3 132 Match the key phrases with theresponses in blue in the dialogue....
1
82
Пошаговое объяснение:
Пусть наше число равно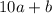 , где
, где  - первая цифра двузначного числа, а
- первая цифра двузначного числа, а 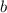 - вторая. Тогда, исходя из первого условия,
- вторая. Тогда, исходя из первого условия, 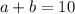 .
.
После перестановки наше число имеет вид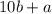 .
.
Тогда, исходя из второго условия,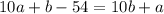 .
.
Получаем систему уравнений:
ответ: исходное число 82
Пошаговое объяснение:
пусть х и у цифры числа, исходное число было 10х+у.
Если цифры поменять местами, то получим число 10у+х.
Вычтем из первого числа второе и получим 54. тогда система уравнений:
х+у=10
10х+у-(10у+х) =54,
х+у=10
9х-9у=54
Система:
х+у=10 (1)
х-у=6 (2) Сложим (1) и (2)
2х=16
х=8
у=2
ответ: 82