1. Математика
  2. Сумма цифр числа, получившегося

Сумма цифр числа, получившегося в результате суммы 1+11+101+1001+10001+...+10...01 (в последнем слагаемом 50 нулей), равна:

Dariailko Dariailko    3   28.08.2021 17:56    13

Ответы
Bluka23 Bluka23  27.09.2021 22:02

Заметим, что в сумме присутствуют числа 1, 11, а также числа с одним нулем, с двумя нулями, и так далее, с 50-ю нулями. Таким образом, в сумме всего записано 52 числа.

Удобно их сложить в столбик:

\begin{array}{r}\underline {+ \begin{array}{r} 1 \\ 11 \\ 101 \\ 1001 \\ 10001 \\ \ldots \\ 1\underset{50}{\underbrace{0\ldots 0}}1\end{array} }\end{array}

Отдельно сложим разряды единиц во всех числах и отдельно все остальные разряды.

Так как в разряде единиц во всех числах стоит 1, то сумма всех единиц равна 52.

Какие-либо разряды, кроме единиц, присутствуют в 51 числе. Поэтому, при суммировании всех остальных разрядов получим число, состоящее из 51 единицы.

\begin{array}{r}\underline {+ \begin{array}{r} 1 \\ 11 \\ 101 \\ 1001 \\ 10001 \\ \ldots \\ 1\underset{50}{\underbrace{0\ldots 0}}1\end{array} }\\\underline {+ \begin{array}{r} 52 \\ \underset{51}{\underbrace{1\ldots 11}}\;\, \end{array} }\end{array}

Сложим два получившихся числа:

\begin{array}{r}\underline {+ \begin{array}{r} 1 \\ 11 \\ 101 \\ 1001 \\ 10001 \\ \ldots \\ 1\underset{50}{\underbrace{0\ldots 0}}1\end{array} }\\\underline {+ \begin{array}{r} 52 \\ \underset{51}{\underbrace{1\ldots 11}}\;\, \end{array} }\\{\begin{array}{r} \underset{50}{\underbrace{1\ldots 1}}62\end{array}\end{array}

Находим сумму цифр числа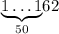 \underset{50}{\underbrace{1\ldots 1}}62:

1\cdot 50+6+2=50+6+2=58

ответ: 58

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
zvezdoska zvezdoska  05.06.2020 15:58
Расположи числа в порядке возрастания: sin41°, sin83°, sin122°, sin162°....
Shermetovelyar552 Shermetovelyar552  04.06.2020 15:53
У кожній клітинці квадрата 3 х 3 записано числа. На жаль, чисел не видню,оскільки вони залиті чорнилом. Однак суми чисел у кожному рядку та суми чисел у двох стовпчиках...
тата246 тата246  04.06.2020 15:53
Установите соответствие между утверждениями (А – В) и видами событий (1 – 4) и дайте ответ. А) В данном опыте событие А не произойдёт. Б) Событие А не может произойти...
Xylinado Xylinado  04.06.2020 15:53
Здравствуйте сделать задания. Буду очень благодарная! Нужно решить со 2 задания и до конца....
goodanonim goodanonim  04.06.2020 15:51
Разложение в ряд Маклорена...
kirill20060729 kirill20060729  04.06.2020 15:50
1)Проверьте правильность следующих утверждения:Произведение чисто мнимого числа на действительное равно чисто мнимому числу. Для проверки возьмите числа: Z1=7i, Z2=3...
nastyabodrova1 nastyabodrova1  04.06.2020 15:49
Найдите общий вид первой функции для функции: f(x)=(x+1)²​...
р6661 р6661  04.06.2020 15:47
Какое количества мешков песка нужно, для того чтобы замесить раствор для заливки 20 столбов столбчатого фундамента размерами 0,5 × 0,5 × 1 м, если в один мешок можно...
kokosha11 kokosha11  04.06.2020 15:47
Найдите значение выражения4,5ѕіn а, если cos a=4 корень 2 делить на 9, 3п делить на 2 a 2п​...
Vikysik4718 Vikysik4718  04.06.2020 15:39
Знайти множину усіх первісних...

Популярные вопросы