Стороны треугольника соответственно равны 9 см, 10 см и 11 см. Найди косинус большего угла треугольника. (Результат округли до сотых (0,01).) cosA= . Какой

Question

Математика: Стороны треугольника соответственно равны 9 см, 10 см и 11 см. Найди косинус большего угла треугольника.  ￼ (Результат округли до сотых (0,01).) cosA= . Какой это треугольник? ответ:тупоугольныйостроугольныйневозможно определитьпрямоугольный​

Варя0601 · Answer

Пусть - это сторона, равная 9 см, 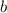- сторона, равная 10 см, - сторона, равная 11 см. Напротив большей стороны лежит больший угол, следовательно, самый большой угол в этом треугольнике, тот, что лежит напротив .

По теореме косинусов:

$c^2 = a^2 + b^2 -2ab\cos\alpha$

$\cos\alpha$ - искомая величина. Выражаем её и вычисляем:

$2ab\cos\alpha = a^2+b^2-c^2\ \ \ \Rightarrow\ \cos\alpha = \dfrac{a^2+b^2-c^2}{2ab} = \dfrac{9^2 + 10^2 - 11^2}{2\cdot 9\cdot 10} =\\\\\\=\dfrac{81+100-121}{180} = \dfrac{60}{180} = \dfrac{1}{3} \approx \boxed{\bf{0,33}}$

Так как самый большой угол данного треугольника имеет положительный косинус, то этот треугольник остроугольный (косинус прямого угла равен нулю, а тупого - отрицателен. Так как у нас косинус самого большого угла в треугольнике положителен, то этот угол является острым).

Популярные вопросы