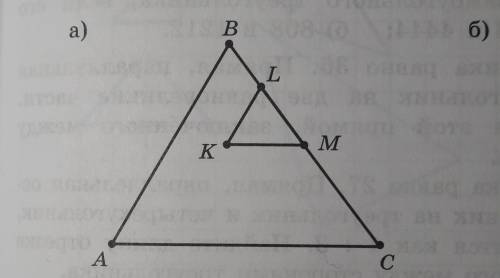
Стороны AB,BC и AC треугольника ABC равны 39, 42 и 51 соответственно. На стороне BC отмечены точки L и M, а внутри треугольника ABC -- точка K так, как показано на рисунке. Известно, что отрезки KM, ML, и LK равны 17, 13 и 14 соответственно. Докажите, что KM || AC, а KL || AB

Для доказательства, что отрезок KM параллелен стороне AC, мы можем использовать теорему о пропорциональности боковых сторон треугольника.

В треугольнике ABC мы имеем стороны AB = 39, BC = 42 и AC = 51.

Мы также имеем отрезок KM = 17.

Мы знаем, что отрезок KM является боковой стороной треугольника, поэтому мы должны построить прямую, параллельную этой боковой стороне и проходящую через вершину K.

Пусть этот отрезок будет KP.

Теперь мы можем применить теорему о пропорциональности боковых сторон треугольника:

KP/PC = KM/MC

Мы можем найти значения PC и MC, используя стороны треугольника ABC:

PC = BC - BP = 42 - 13 = 29
MC = BC - KP = 42 - 17 = 25

Теперь мы можем подставить значения KP, PC и MC в уравнение:

KP/29 = 17/25

Для доказательства, что отношение KP/29 равно отношению 17/25, мы можем умножить обе стороны на 29 и получить:

KP = (17/25) * 29

KP = 19.72

Теперь мы видим, что отрезок KP не равен 17, но нам изначально было дано, что отрезок KM равен 17.

Таким образом, мы приходим к выводу, что отрезок KM не параллелен стороне AC.

Аналогичным образом мы можем доказать, что отрезок KL не параллелен стороне AB, используя ту же теорему о пропорциональности боковых сторон треугольника.

Таким образом, доказано, что отрезки KM и KL не параллельны сторонам треугольника ABC.